Introducción
Como se ha comentado en otros artículos de esta web, Análisis de series temporales en r, las series temporales son datos expresados como una secuencia de puntos, sobre un periodo de tiempo. Realizar un análisis de datos de series temporales permite encontrar modelos o tendencias para predecir valores futuros que ayuden, a la hora de tomar decisiones, a qué estas sean más efectivas y óptimas.
¿Cómo Analizar una Serie Temporal? (mas info)
- Dominio Temporal
- Auto-Correlación
- Correlación Cruzada
- Dominio Frecuencial
- Análisis Espectral
- Análisis de Armónicos
Además las series temporales se pueden clasificar en:
- Lineales o no lineales
- Discretas o Continuas
- Univariante o Multivariante
y en función de la técnica de análisis usada:
- ARIMA
- Box-Jenkins multivariante
- Metodos Holt Winters de suavización exponencial (simple, doble y triple)
MODELO ARIMA
ARIMA son las siglas de AutoRegressive Integrated Moving Average. Regresión Automática (AR) es el término que hace referencia a los retardos de las series diferenciadas (T-i), Media Móvil (MA) hace referencia a los retardos de los errores y la integración (I) es el número de diferencias usadas para hacer que la serie de tiempos sea estacionaria.
Condiciones Necesarias para el Modelo ARIMA
- Los datos deben ser estacionarios, esto significa que las propiedades de la serie no dependen del momento en que se capturan. Una serie de ruido blanco y series con comportamiento cíclico también pueden considerarse series estacionarias.
- Los datos deben ser univariantes, ARIMA trabaja en una sola variable. La regresión automática tiene que ver con la regresión de los valores pasados.
Para definir un modelo ARIMA vamos a seguir una serie de pasos:
- Análisis exploratorio
- Ajuste del modelo
- Medidas de diagnóstico.
Comenzaremos modelando los datos de una serie temporal. Usando R, convertiremos los datos disponibles en formato de datos de serie temporal. Para hacer esto, ejecutaremos el siguiente comando:
RawData=scan('https://www.diegocalvo.es/wp-content/uploads/2016/09/datos-serie-temporal.txt')
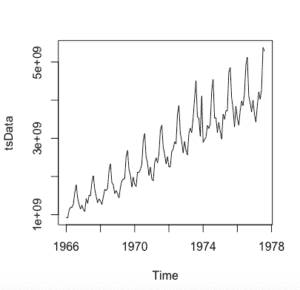
plot(RawData)
tsData = ts(RawData, start = c(1966,1), frequency = 12)
print(tsData)
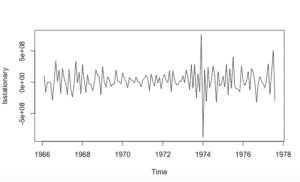
plot(tsData)donde RawData son los datos univariantes que convertimos en serie temporal. start comienza el inicio de los tiempo de los datos, en este caso es enero de 1996 y como los datos son mensuales ‘frequency=12’.
Este es el estado del dataset:
Podemos deducir del gráfico en sí mismo que los puntos de datos siguen un patrón de subidas y caídas en una tendencia ascendente. Ahora necesitamos hacer un análisis para averiguar la no estacionariedad exacta y la estacionalidad en los datos.
Análisis Exploratorio de Datos (EDA)
- Análisis de autocorrelación para examinar la dependencia en serie. Se utiliza para estimar qué valor en el pasado tiene una correlación con el valor actual. Proporciona la estimación p, d, q para los modelos ARIMA.
- Análisis espectral para examinar el comportamiento cíclico. Se realiza para describir cómo la variación en una serie temporal puede ser explicada por componentes cíclicos. También se conoce como un análisis en dominio de la frecuencia. Usando esto, los componentes periódicos en un ambiente ruidoso se pueden separar.
- Estimación y descomposición de la tendencia. Se utiliza para el ajuste estacional. Busca construir, a partir de una serie temporal observada, una serie de componentes (que podrían usarse para reconstruir la serie original) donde cada una de ellas tiene una característica determinada.
Antes de realizar cualquier EDA en los datos, debemos comprender los tres componentes de los datos de una serie temporal:
- Tendencia: un aumento o disminución a largo plazo de los datos se denomina tendencia. No tiene porque ser necesariamente lineal. Es el patrón subyacente en los datos a lo largo del tiempo.
- Estacional o Periódico: cuando una serie está influenciada por factores estacionales, es decir, un trimestre del año, mes o días de una semana, la estacionalidad existe en la serie. Siempre es de un período fijo y conocido. P.ej. – Un aumento repentino en las ventas durante el verano, etc.
- Cíclico: cuando los datos muestran subidas y caídas que no son del período fijo, lo llamamos patrón cíclico. Por ejemplo – La duración de estas fluctuaciones suele ser de al menos 2 años.
En R podemos averiguar estos componentes de la serie temporal con los siguientes comandos:
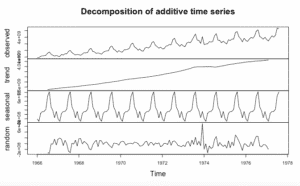
componentes.ts = decompose(tsData)
plot(componentes.ts)La salida se parecerá a la siguiente:
En este gráfico podemos observar 4 sub-graficos:
- Observed: los datos actuales
- Trend: el movimiento general hacia arriba o hacia abajo de los puntos de datos
- Seasonal: cualquier patrón mensual / anual de los puntos de los datos
- Random – parte inexplicable de los datos
Observando de cerca cada uno de estos gráficos, podemos descubrir si los datos satisfacen todos los supuestos del modelado ARIMA, principalmente, la estacionariedad y la estacionalidad.
A continuación, debemos eliminar la parte no estacionaria de ARIMA. Para facilitar el análisis aquí, también eliminaremos la parte estacional de los datos. La parte estacional puede eliminarse del análisis y agregarse más tarde, o puede tratarse en el propio modelo ARIMA.
Para conseguir estacionariedad:
- diferencia los datos – calcula las diferencias entre observaciones consecutivas
- aplica el logaritmo o raíz cuadrada a los datos de la serie para estabilizar la varianza no constante
- Si los datos contienen una tendencia, ajusta algún tipo de curva a los datos y luego modela los residuales de ese ajuste.
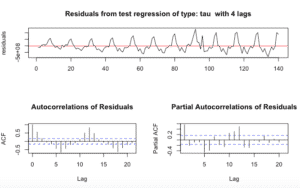
- Prueba de raíz unitaria: esta prueba se usa para descubrir la primera diferencia o regresión que se debe usar en los datos de tendencias para hacerla estacionaria. En la prueba Kwiatkowski-Phillips-Schmidt-Shin (KPSS), los valores pequeños de p sugieren que se requiera una diferenciación.
El codigo R para la prueba de raíz unitaria:
#install.packages("fUnitRoots")
library("fUnitRoots")
urkpssTest(tsData, type = c("tau"), lags = c("short"),use.lag = NULL, doplot = TRUE)La salida será algo como esto:
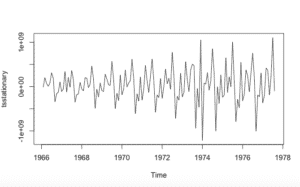
Después eliminamos la no estacionariedad:
tsstationary = diff(tsData, differences=1)
plot(tsstationary)Hay diversos gráficos y funciones que nos pueden ayudar a detectar la estacionalidad:
- Un diagrama de subseries estacional
- Diagrama de caja múltiple
- Gráfico de autocorrelación
- ndiffs () se utiliza para determinar el número de primeras diferencias necesarias para que las series temporales no sean estacionales
Codigo R para calcular la autocorrelación:
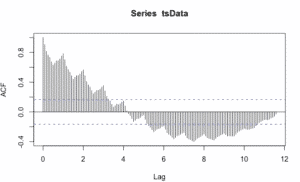
acf(tsData,lag.max=140)La función de autocorrelación (acf ()) proporciona la autocorrelación en todos los retrasos posibles. La autocorrelación en el retraso 0 se incluye por defecto, lo que siempre toma el valor 1, ya que representa la correlación entre los datos y ellos mismos. Como podemos observar en el gráfico anterior, la autocorrelación continúa disminuyendo a medida que aumenta el retraso, lo que confirma que no existe una asociación lineal entre las observaciones separadas por retrasos mayores.
timeseriesseasonallyadjusted <- tsData-componentes$seasonal
tsstationary <- diff(timeseriesseasonallyadjusted, differences=1)Para eliminar la estacionalidad de los datos, restamos el componente estacional de la serie original(media cero) y luego lo diferenciamos para que sea estacionario ( varianza constante e independiente).
Después de eliminar la estacionalidad y hacer que los datos sean estacionarios, se verá así:
plot(tsstationary)El suavizado se hace generalmente para ayudarnos a ver mejor los patrones, las tendencias en las series temporales. Generalmente alisa las irregularidades para ver una señal más clara. Para datos estacionales, podríamos suavizar la estacionalidad para que podamos identificar la tendencia. El suavizado no nos proporciona un modelo, pero puede ser un buen primer paso para describir varios componentes de la serie.
Para suavizar las series de tiempo:
- Promedio móvil ordinario (único, centrado): en cada punto del tiempo determinamos los promedios de los valores observados que preceden a un tiempo determinado. Para eliminar la estacionalidad de una serie, para que podamos ver mejor una tendencia, usaríamos un promedio móvil con una longitud = lapso estacional. El lapso estacional es el período de tiempo después del cual se repite una estacionalidad, por ejemplo, – 12 meses si se nota estacionalidad cada mes de diciembre. Por lo tanto, en la serie suavizada, cada valor suavizado se ha promediado a lo largo del período de la temporada completa.
- Promedio ponderado exponencialmente: en cada punto del tiempo, aplica factores de ponderación que disminuyen exponencialmente. La ponderación de cada dato anterior disminuye exponencialmente y nunca llega a cero.
Ajuste del modelo
Una vez que tenemos los datos listos y han satisfecho todas las suposiciones del modelo, para determinar el orden del modelo que se ajustará a los datos, necesitamos tres variables: p, d y q que son enteros positivos que se refieren al orden de las partes medias autorregresivas, integradas y móviles del modelo, respectivamente.
Para identificar que valores de p y q serán apropiados, necesitamos ejecutar las funciones acf() y pacf()
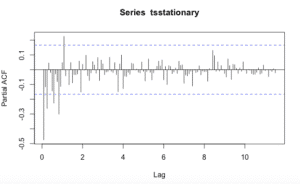
pacf () en el retardo k-esimo es la función de autocorrelación que describe la correlación entre todos los puntos de datos que están exactamente k pasos antes, después de tener en cuenta su correlación con los datos entre esos k pasos. Ayuda a identificar el número de coeficientes de autorregresión (AR) (valor p) en un modelo ARIMA.
El código R para ejecutar los comandos acf() y pacf():
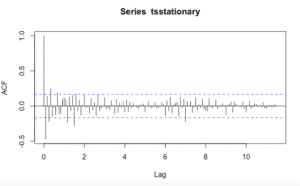
acf(tsstationary, lag.max=140)pacf(tsstationary, lag.max=140)Obtenemos las siguientes gráficas:
La forma de acf () para definir valores de p y q es mirar los gráficos y repasando la tabla podemos determinar qué tipo de modelo seleccionar y cuáles serán los valores de p, d y q.
| Forma | Modelo |
| Serie exponencial decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Picos alternativos positivos y negativos, decayendo a 0 | Modelo Auto Regresivo (AR). Función pacf () que se utilizará para identificar el orden del modelo |
| Uno o más picos en serie, resto todos son 0 | Modelo de media móvil (MA), identifica el orden donde el gráfico se convierte en 0 |
| Después de algunos retrasos en general la serie va decayendo. | Modelo mezclado AR & MA |
| La serie total es 0 o casi 0 | Datos aleatorios |
| Valores medios a intervalos fijos | Necesitamos incluir el término AR de estacionalidad |
| Picos visibles que no decaen a 0 | Series no son estacionarias |
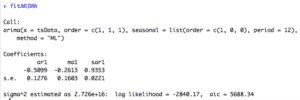
fitARIMA <- arima(tsData, order=c(1,1,1),seasonal = list(order = c(1,0,0), period = 12),method="ML")
#install.packages("lmtest")
library(lmtest)
coeftest(fitARIMA)orden especifica la parte no estacional del modelo ARIMA: (p, d, q) se refiere al orden AR, el grado de diferencia y la orden MA.
estacional especifica la parte estacional del modelo ARIMA, más el período (que por defecto es la frecuencia (x), es decir, 12 en este caso). Esta función requiere una lista con el orden de los componentes pero dado en un vector numérico de longitud 3, y el período.
el método se refiere al método de ajuste, que puede ser «probabilidad máxima (ML)» o «minimizar la suma de cuadrados condicional (CSS)». El valor predeterminado es la suma de cuadrados condicional.
El proceso de ajuste es un proceso recursivo y necesitamos ejecutar esta función arima () con diferentes valores (p, d, q) para encontrar el modelo más optimizado y eficiente.
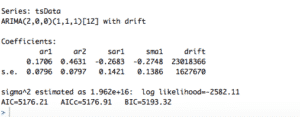
La salida de fitarima () incluye los coeficientes ajustados y el error estándar para cada coeficiente. Observando los coeficientes podemos excluir los insignificantes. Podemos usar una función confint () para este propósito. Podemos usar una función confint () para este propósito.
confint(fitARIMA)
Elección del mejor modelo
R utiliza la estimación de máxima verosimilitud (MLE) para estimar el modelo ARIMA. Intenta maximizar la probabilidad logarítmica para valores dados de p, d y q al encontrar estimaciones de parámetros para maximizar la probabilidad de obtener los datos que hemos observado. Averigüa el Criterio de Información de Akaike (AIC) para un conjunto de modelos e investigarlos modelos con los valores AIC más bajos. Prueba el criterio de información bayesiano (BIC) de Schwarz e investiga los modelos con los valores BIC más bajos. Al estimar los parámetros del modelo utilizando la estimación de máxima verosimilitud, es posible aumentar la probabilidad agregando parámetros adicionales, lo que puede resultar en un ajuste excesivo. El BIC resuelve este problema introduciendo un término de penalización para el número de parámetros en el modelo. Junto con AIC y BIC, también debemos observar de cerca los valores de los coeficientes y debemos decidir si incluir ese componente o no de acuerdo con su nivel de significación.
Medidas de diagnostico
Deben observarse los coeficientes de autocorrelación muestral de los residuos y comprobar que ninguno de ellos supera el valor de las bandas de significatividad al 5% (±1,96(1/T1⁄2)). El valor T1⁄2 es una aproximación de la varianza asintótica pero resulta sólo adecuada para valores grandes de «j». Se aconseja,por tanto, utilizar distinta amplitud de bandas como por ejemplo ±(1/T1⁄2) para los términos más cercanos a cero.Intenta averiguar el patrón en los residuos del modelo elegido trazando el ACF de los residuos y haciendo una prueba de portmanteau. Necesitamos probar modelos modificados si la gráfica no parece un ruido blanco. Una vez que los residuos parezcan ruido blanco, calcularemos los pronósticos.
Prueba de Box-Ljung
Es una prueba para comprobar si una serie de observaciones en un período de tiempo especifico son aleatorias o independientes en todos los retardos hasta el especificado. En lugar de probar la aleatoriedad en cada retardo distinto, prueba la aleatoriedad «general» basada en un número de retardos y, por lo tanto, es una prueba de comparación. Se aplica a los residuos de un modelo ARIMA ajustado, no a la serie original, y en tales aplicaciones, la hipótesis que se está probando realmente es que los residuos del modelo ARIMA no tienen autocorrelación.
Si los retardos no son independientes, un retardo puede estar relacionado con otros retardos k unidades de tiempo después por lo que la autocorrelacion puede reducir la exactitud de un modelo predictivo basado en el tiempo y conducir a una interpretación errónea de los datos.
El código R para obtener los resultados de la prueba Box:
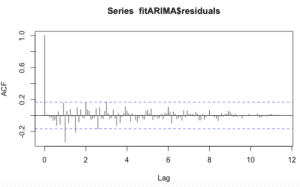
acf(fitARIMA$residuals,lag.max=140)
#install.packages("FitAR")
library(FitAR)
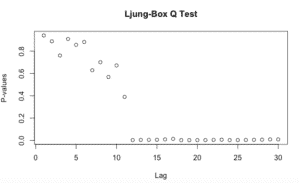
boxresult=LjungBoxTest (fitARIMA$residuals,k=2,StartLag=1)
plot(boxresult[,3],main= "Ljung-Box Q Test", ylab= "P-values", xlab= "Lag")
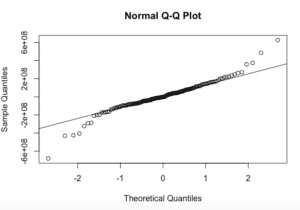
qqnorm(fitARIMA$residuals)
qqline(fitARIMA$residuals)La salida:
El ACF de los residuos muestra autocorrelaciones no significativas.
Todos los valores de p para la prueba Ljung-Box Q están muy por encima de 0.05 , lo que nos indica que los datos no son dependientes.
Los valores son normales ya que descansan en una línea y no están por todos lados.
Como todos los gráficos apoyan el supuesto de que no hay un patrón en los residuales, podemos seguir adelante y calcular el pronóstico.
Función auto.arima ():
El paquete de pronóstico proporciona dos funciones: ets () y auto.arima () para la selección automática de modelos exponenciales y modelos ARIMA.
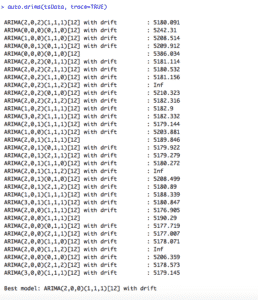
La función auto.arima () en R utiliza una combinación de pruebas de raíz unitaria, minimización del AIC y MLE para obtener un modelo ARIMA.
La prueba KPSS se usa para determinar el número de diferencias (d) En el algoritmo Hyndman-Khandakar para el modelado ARIMA automático.
Los p, d y q luego se eligen minimizando el AICc. El algoritmo utiliza una búsqueda por pasos para recorrer el espacio del modelo para seleccionar el mejor modelo con el AICc más pequeño.
Si d = 0, entonces se incluye la constante c; si d≥1 entonces la constante c se pone a cero. Las variaciones en el modelo actual se consideran variando p y / o q del modelo actual en ± 1 e incluyendo / excluyendo c del modelo actual.
El mejor modelo considerado hasta ahora (ya sea el modelo actual o una de estas variaciones) se convierte en el nuevo modelo actual.
Ahora, este proceso se repite hasta que no se pueda encontrar un AIC inferior.
#install.packages("forecast")
library(forecast)
auto.arima(tsData, trace=TRUE)
Predecir utilizando un modelo ARIMA
Los parámetros del modelo ARIMA se pueden usar como un modelo predictivo para hacer pronósticos de valores futuros de las series temporales, una vez que se selecciona el modelo más adecuado para los datos de la serie temporal.
El valor d afecta a los intervalos de predicción; los intervalos de predicción aumentan de tamaño con valores más altos de «d». Todos los intervalos de predicción serán esencialmente los mismos cuando d = 0 porque la desviación estándar de la previsión a largo plazo irá a la desviación estándar de los datos históricos.
Existe una función llamada predict () que se usa para predicciones a partir de los resultados de varias funciones de ajuste de modelos. Se necesita un argumento n.ahead () que especifica la cantidad de tiempo que se adelanta para predecir.
predict(fitARIMA,n.ahead = 5)La función forecast() en el paquete R de forecast también se puede utilizar para pronosticar valores futuros de la serie temporal. Aquí también podemos especificar el nivel de confianza para los intervalos de predicción utilizando el argumento de nivel.
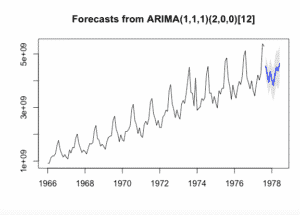
futurVal <- forecast(fitARIMA,h=10, level=c(99.5))
plot(futurVal)Los pronósticos se muestran como una línea azul, con los intervalos de predicción del 80% como un área sombreada oscura, y los intervalos de predicción del 95% como un área sombreada clara. Este es el proceso general analizar para analizar datos de series temporales y pronosticar valores de las series existentes utilizando ARIMA.






Excelente, eres muy amable. Saludos
Gracias bro, sds
Un agradecido, hacia mucho que no visitaba temas sobre Series de Tiempo porque mi área de especialización es otra: los diseños d muestreo y de experimentos (particularmente la primera). He recibido una solicitud de ayuda de un colega sobre el tema razón por la cual estoy realizando una exploración bibliográfica y creo que su trabajo me será de gran utilidad para ayudar a mi amigo, aparte de recordar y volver a encontrarme con esta área del conocimiento de tanta utilidad y uso.
Atte.
Hernán Miranda P.
Hola, me gustaría saber como asignar el Lag 12? si escribo Order(12,0,0) me tira doce, y lo que quisiera solo el 12.
como puedo hacer auto.arima sin utilizar esa funcion, es decir cual seria un ejemplo de un codigo que de resultados automaticos de arima, sin tener que usar la funcion auto.arima?
si quieres correr cualquier modelo utiliza el comando arma( datos, order=c(p,d,q))
Felicitaciones
Gracias
Muchas gracias, me ayudo mucho a entender el tema de Análisis con ARIMA.
Gracias!! en el modelo ARIMA ,¿Cómo se calcula la suma de los pronósticos? y una mas ¿Cómo se calcula el error MAPE del del modelo?,gracias de nuevo
Muchas gracias por su excelente trabajo que nos ayuda a comprender un poco más sobre estos temas.
Buenas tardes, estoy trabajando sobre una serie temporal que no es estacionaria, y tras aplicarle logaritmos y 1 Dif estacional y 1 Dif regular, y hacer el acf y pacf me han recomendado realizar otra diferencia estacional, pero me sale algo raro.
Alguien me podría ayudar?
Gracias de antemano!!!!
Hola. El paquete FitAR se eliminó, cómo poder reemplazar ese paso?
Gracias.