Uso: Clasificador de clases por clustering o agrupamiento, no supervisado.
Descripción: El objetivo es segmentar un conjunto de datos en grupos homogéneos, disjuntos entre sí, es decir, ningún elemento formará parte de dos grupos distintos, por lo que, serán heterogéneos entre sí.
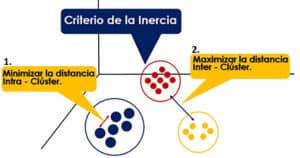
Para ello, el algoritmo utiliza el Criterio de la Inercia, que indica que el modelo será óptimo, cuando los grupos formados tengan una distancia mínima intra-cluster y, una distancia máxima inter-cluster, como se observa en el siguiente gráfico.
Los grupos que se formaran serán por compartir características similares, por lo cual, por ser un método no supervisado el Científico de Datos deberá darle una interpretación a la clasificación realizada.
Para ello, el algoritmo identificara k centroides, los cuales compararán su valor medio con el de los datos restantes, seleccionando aquellos más cercanos para realizar los clúster o agrupamiento.
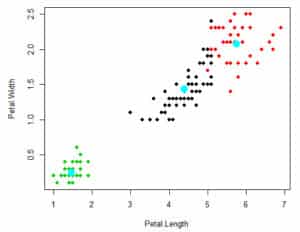
En el siguiente gráfico se puede evidenciar los centroides del ejemplo que estamos presentando utilizando como variables de aporte de información: Petal.Width y Petal.Length.
Variable dependiente: no métricas.
Variables independientes: métricas.
Ejemplo en R: Clasificar tipo de flor atendiendo a sus características físicas como pueden ser el ancho y alto de los pétalos y sépalos.
Aplicaciones: Segmentación de Mercados, Geoestadística, Astronomía y Agricultura.
# La función kmeans viene por defecto en la librería: stat. set.seed(12345) #Invocamos la Base de datos Iris. data(iris) datos=iris # Verificamos la composición del set de datos. # En este caso hay 5 variables: 4 numéricas (Sepal y Petal) y 1 categorica determinada como factor (Species). str(datos)
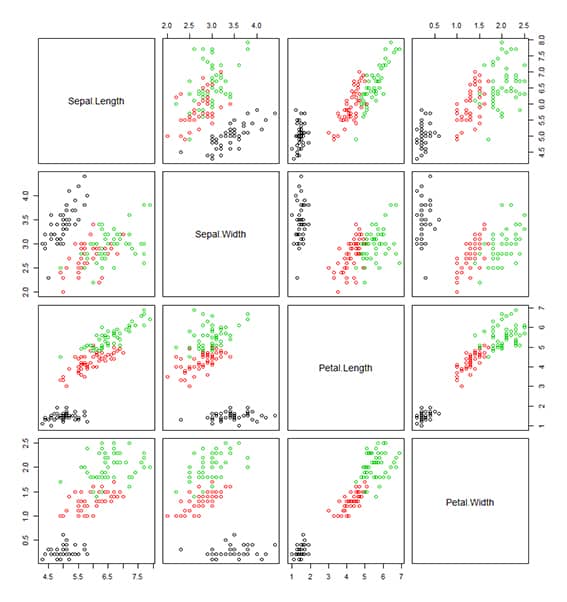
# En este caso la variable objetivo, nuestra y, que es la variable: Species. datos$Species # Las primeras 50 son: Setosas, las 50 siguientes son: Versicolor y, las ultimas 50, son: virginica y, estas conforman las 3 CLASES a pronosticar. # Gráfico de dispersión de las clases según las variables predictoras. pairs(datos[-5],col=datos$Species) # Verificamos la correlación entre las variables NUMÉRICAS existentes. correlacion=cor(datos[-5]) correlacion # Con esto podemos observar que combinación de variables van a portar mayor información a la formación de los grupos. En este caso podemos observar que la combinación Petal.Width y Petal.Length, nos proporciona la mejor clusterización.
# Aplicación del Método: K MEANS. # El objetivo del Kmeans o K medias es formar grupos homogéneos, distintos entre si. En este caso, nuestro k=3, formaremos 3 grupos, porque ya conocemos que hay 3 distintos tipos de iris, sin embargo, el n, dependerá del problema. grupos=kmeans(datos[-5],3) # La función kmeans recibe dos parametros: datos (solo las variables numericas) y k (número de grupos a formar). grupos # El número 3: corresponde a las Setosas, el número 2 a las Versicolor y el número 1 a las Virginicas. # Con la siguiente sentencia se obtiene el grupo al cual pertenecen los registros o filas del set de datos según la función: kmeans . grupos$cluster # Como se puede apreciar se han formado 3 clusters o grupos. # Grupo 3, corresponden a: Setosas. # Grupo 1, corresponden a: Versicolor. # Grupo 2: corresponden a: Virginica.
Enfoque en el Output:
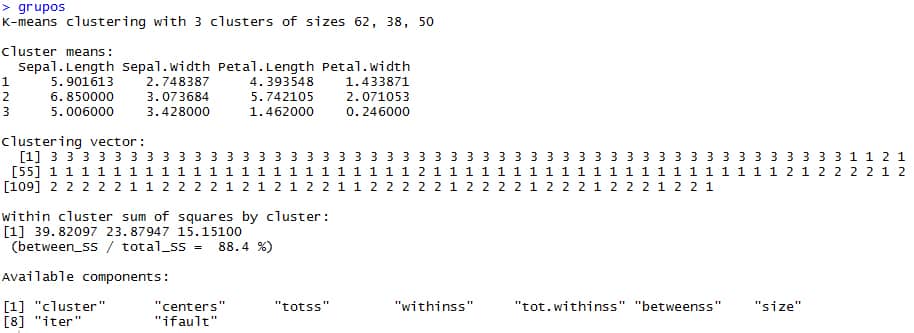
# K-means clustering with 3 clusters of sizes 62, 38, 50 # Hay 3 clúster de 62,38 y 50 datos cada uno para un total de 150 registros, lo mismo que teniamos al inicio, pero 50 eran setosas, 50 eran versicolor y 50 eran virginicas. # Esta imprecisión es por el error asociado a cada modelo. Cluster means: Sepal.Length Sepal.Width Petal.Length Petal.Width 1 5.901613 2.748387 4.393548 1.433871 2 6.850000 3.073684 5.742105 2.071053 3 5.006000 3.428000 1.462000 0.246000 # El algoritmo computa la media más optima para hallar los centroides, los cuales, muestra en Cluster Means, cuando detecta estos, en este caso son 3, porque k=3. Clustering vector: [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 1 2 1 [55] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 2 2 2 1 2 [109] 2 2 2 2 2 1 1 2 2 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 2 1 2 2 2 2 1 2 2 2 1 2 2 2 1 2 2 1 # En Clustering vector, se indica el pronostico para cada registro testeado con el algoritmo. Within cluster sum of squares by cluster: [1] 39.82097 23.87947 15.15100 (between_SS / total_SS = 88.4 %) # between_SS / total_SS, es una medida de calidad e indica que tanto están separados los grupos de manera inter-cluster en relación al agrupamiento intra-cluster, mientras, se esté más cercano al 100%, mayor será la calidad del modelo. # [1] 39.82097 23.87947 15.15100, es la inercia intra-clúster de cada grupo. # Available components: # [1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size" # [8] "iter" "ifault" # Son los elementos disponibles del modelo, los cuales, se explican a continuación: 1. Cluster: La categorización asignada a cada observación del dataset en función a su cercanía a estos centros. 2. Centers: Los centroides. 3. Totss: Inercia total del conjunto de datos. 4. Withinss: Inercia intra-clases de cada uno de los grupos. 5. Tot.withinss: Inercia intra-clases total. 6. Betweenss: Inercia inter-clases. 7. Size: El tamaño de cada grupo. 8. Iter: Número de iteraciones empleado.
# Evaluación de Resultados
# Asignamos a la variable: clases, los datos numéricos como factor del set de datos.
clases=factor(datos[,5])
# Asignamos a la variable: predicho, las clases predichas por el kmedias.
predicho= NULL
# La función: mode (moda), contará la cantidad de registros clasificados como: setosa, versicolor o virginica en cada llamada y, retornará la mayor cantidad de ocurrencias vinculadas a la clase que se le asigne.
mode=function (x){
ux=unique(x)
ux[which.max(tabulate(match(x,ux)))]
}
# Segmentamos el clustering vector de 50 en 50, hasta llegar a 150, es decir, 3 grupos de 50, porque, al inicio, habian 50 flores de cada tipo: Setosas, Versicolor y Virginica.
# ¡ Importante ! : # Evidentemente el algoritmo tiene errores en clasificar entre Versicolor y Virginica, por lo cual, se necesita conocer la precisión y el error asociado al modelo. # Setosas # [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 # Versicolor # 1 1 2 1 # [55] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 # Virginicas # 2 1 2 2 2 2 1 2 # [109] 2 2 2 2 2 1 1 2 2 2 2 1 2 1 2 1 2 2 1 1 2 2 2 2 2 1 2 2 2 2 1 2 2 2 1 2 2 2 1 2 2 1
# Así pues, las primeras 50 eran: Setosas, las 50 siguientes eran: Versicolor y, las ultimas 50, eran: virginica y, estas conforman las 3 CLASES a pronósticar. predicho [grupos$cluster==mode(grupos$cluster[1:50])]="setosa" predicho [grupos$cluster==mode(grupos$cluster[50:100])]="versicolor" predicho [grupos$cluster==mode(grupos$cluster[100:150])]="virginica"
# ¡ Importante ! : # Verificar que el orden de los grupos son los que se evaluaron al inicio.
# Se transforma la variable: predicho, a factor. predicho=factor(predicho) # Matriz de confusión MC = table(clases, predicho) MC precision=(sum(diag(MC)))/sum(MC) precision error=1-precision error
# En este caso sabíamos cuantos grupos podíamos formar, sin embargo, para otras aplicaciones donde no se sepa correctamente cuántos grupos formar es necesario realizar el test que indicaremos en otra entrega.




0 comentarios