Uso: Clasificador lineal.
Descripción: El análisis de la regresión es una técnica estadística para estimar las relaciones que existen entre variables.
En este modelo se fija la variable que se quiere predecir (variable dependiente) y se determina la relación con el resto de variables predictoras (independientes)
La técnica de regresión lineal simple, esa definida por una ecuación lineal y consta de una serie de pasos, a continuación se muestra un ejemplo en el que se quiere determinar el número de cajas organizadas por un operario con respecto al tiempo que dedica.
Variable dependiente: Métrica.
Variables independientes: Métricas y/o no métricas.
Ejemplo en R: Determinar el tiempo necesario para organizar diferentes bloques de cajas.
Paso 1: Carga de datos inicial
datos <- read.table("https://www.diegocalvo.es/wp-content/uploads/2016/09/datos-regresion-lineal-simple.txt", header = TRUE) names(datos) # Comprobación de cabeceras View(datos) # Comprobación de la carga de datos.
Paso 2: Representar ambas variables gráficamente (diagrama de dispersión) y mediante la observación de la nube de puntos ver a groso modo si existe correlación.
plot(datos$Tiempo,datos$N_Cajas)
Paso 3: Una vez visto que visualmente existe relación debemos intentar modelizar esta relación, en este caso primeramente probaríamos con el modelo más sencillo que es ver si se ajusta a una recta Y=mx+n.
Para estimar los parámetros de la recta nos centraremos en el modelo de mínimos cuadrados por ser el de más amplia aceptación, aunque existan otros como el de máxima verosimilitud.
modelo <- lm(Tiempo ~ N_Cajas, data=datos)
summary(modelo)
Call:
lm(formula = N_Cajas ~ Tiempo, data = datos)
Residuals:
Min 1Q Median 3Q Max
-10.6583 -1.6018 -0.1821 2.5262 5.3952
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.5452 3.4142 5.432 0.000115 ***
datos$N_Cajas 0.6845 0.1805 3.791 0.002244 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.053 on 13 degrees of freedom
Multiple R-squared: 0.5251, Adjusted R-squared: 0.4886
F-statistic: 14.37 on 1 and 13 DF, p-value: 0.002244Al realizar este análisis los parámetros de la ecuación de la recta de mínimos cuadrados que relaciona el número de cajas organizadas con el tiempo utilizado para ello, se obtiene la recta Y = 0,6845 * X + 18,5452
Paso 4: Que la recta se ajuste a los datos no significa que el modelo sea correcto, depende del uso que queramos darle.
Si sólo pretendemos hallar la relación entre dos variables, con calcular la recta de mínimos cuadrados es suficiente.
Si queremos verificar que tenga una buena relación lineal, con el fin de inferir/predecir con la recta de regresión debemos comprobar que se verifican unas reglas ya establecidas y aceptadas que aseguran que nuestro modelo es bueno, para su verificación realizaremos los siguientes análisis:
- Análisis de la correlación
Paso 5: Correlación – mide el grado de relación lineal, calculamos la matriz de coeficientes de correlación:
cor(datos)
N_Cajas Tiempo
N_Cajas 1.0000000 0.7246466
Tiempo 0.7246466 1.0000000Esta correlación es la forma abreviada del coeficiente de correlación de Pearson, la fórmula de utilización original sería:
cor.test(datos$Tiempo,datos$N_Cajas, method = "pearson")
Pearson's product-moment correlation
data: datos$Tiempo and datos$N_Cajas
t = 3.7914, df = 13, p-value = 0.002244
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.3377656 0.9020572
sample estimates:
cor
0.7246466
Se puede afirmar que la correlación es fuerte debido a que tiene un p-valor menor que 0,05 concretamente 0,002244.
- Análisis de los residuos:
Paso 6: Normalidad – Los errores deben seguir una distribución normal
residuos<-rstandard(modelo) # residuos estándares del modelo ajustado (completo) par(mfrow=c(1,3)) # divide la ventana en una fila y tres columnas hist(residuos) # histograma de los residuos estandarizados boxplot(residuos) # diagrama de cajas de los residuos estandarizados qqnorm(residuos) # gráfico de cuantiles de los residuos estandarizados qqline(residuos) par(mfrow=c(1,1)) # devuelve la pantalla a su estado original
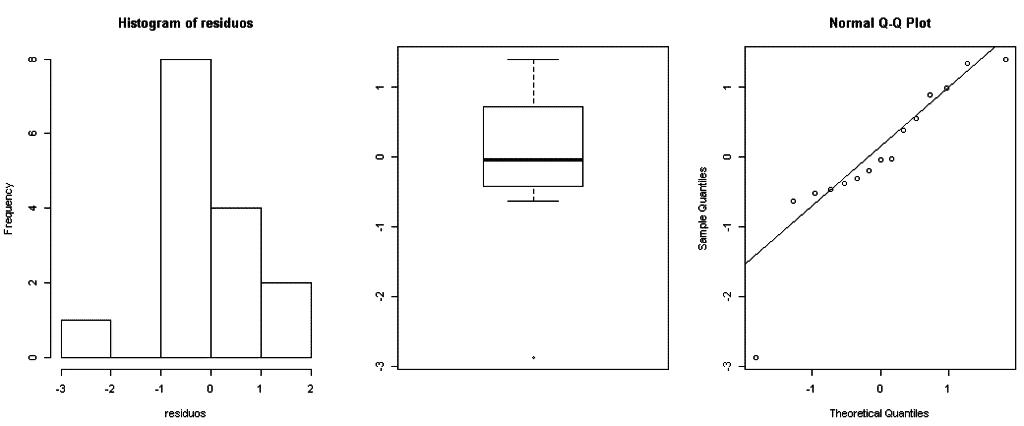
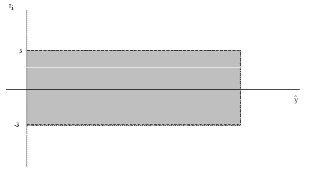
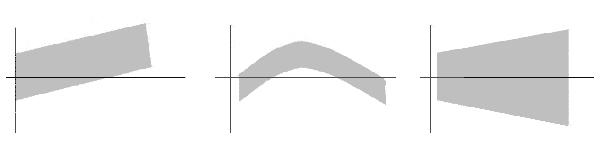
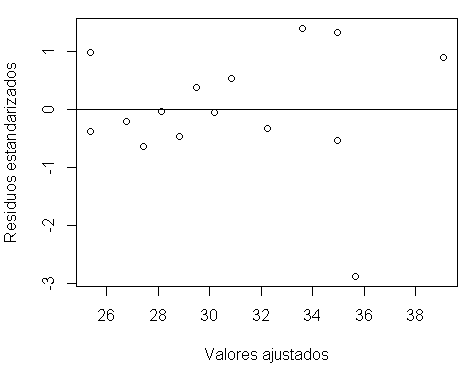
Paso 7: Varianza constante – La varianza de los errores es constante
plot(fitted.values(modelo),rstandard(modelo), xlab="Valores ajustados", ylab="Residuos estandarizados") # gráfico 2D de los valores ajustados vs. los residuos estandarizados abline(h=0) # dibuja la recta en cero
Paso 8: Valores atípicos – La independencia de los errores
plot(datos$N_Cajas,rstandard(modelo),xlab="N_cajas",ylab="Residuos estandarizados")
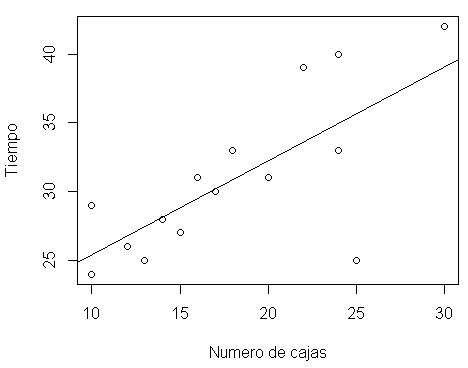
Paso 9: Visualización de la regresión
plot(datos$N_Cajas, datos$Tiempo ,xlab = "Numero de cajas", ylab = "Tiempo" )
abline(modelo)

Paso 10: Predicción de la variable dependiente respecto a los valores que puede tomar la variable independiente
tiempo_estimado <- data.frame(N_Cajas = 24) prediccion <-predict(modelo, tiempo_estimado) prediccion 1 34.97381
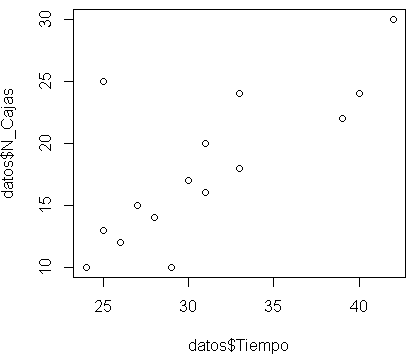
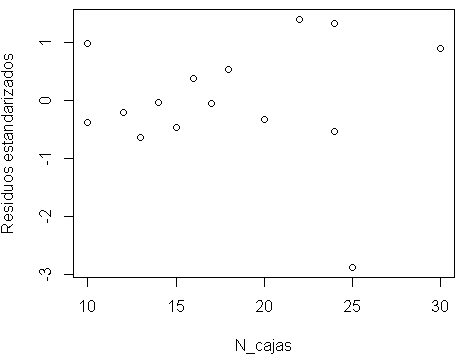




Hola Diego
Excelente aporte me sirvió demasiado con respecto a un tema en clase
Tu sitio Web es grandioso
Saludos!!
Buen trabajo
Muchas gracias
Hola
Gracias por tu aportación
Podrás subir algo relacionado métodos para corregir la heterocedasticidad?
En el grafico del paso 9 debe ser tiempo cajas primero y luego segundo ncajas
*En el grafico del paso 9 debe ser tiempo primero y luego segundo ncajas
Muy bueno
HOLA; MUUY BUENA LA EXPLICACION. ME PODRÍAS DECIR COMO DEBERÍA SER LA SENTENCIA DEL PASO 10, SI QUISIERA LA PREDICCION PARA 24 Y 30 CAJAS?
GRACIAS
¿Por qué en el paso 9 aparecen las cajas en x?
Gracias