Uso: Clasificador lineal o para la reducción de dimensiones antes de una clasificación.

Descripción: Análisis Discriminante Lineal o ADL es un método utilizado para el reconocimiento de patrones y aprendizaje de máquinas para encontrar una combinación lineal de rasgos que caracterizan varias clases de objetos.

Variable dependiente: no métricas.

Variables independientes: métricas.

Ejemplo en R: Clasificar tipo de flor atendiendo a sus características físicas como pueden ser el ancho y alto de los pétalos y sépalos.

# Carga de datos inicial, tipos de flores con diferentes caracteristicas 
data(iris)
datos <- iris
View(datos)

# Selección de una submuestra de 105 (el 70% de los datos)
set.seed(101)
tamano.total <- nrow(datos)
tamano.entreno <- round(105*0.7)
datos.indices <- sample(1:tamano.total , size=tamano.entreno)
datos.entreno <- datos[datos.indices,]
datos.test <- datos[-datos.indices,]

# Carga de librerías
require(MASS) # para lda()
require(klaR) # para errormatrix() y stepclass()

# Ejecución del análisis discriminante
datos.entreno.lda <- lda(formula= Species~. , data=datos.entreno)

# Asignación a cada clase, proporciona la probabilidad de pertenencia a cada una
datos.entreno.lda.p <- predict(datos.entreno.lda, newdata=datos.test, interval='confidence')

# Asignación de colores a cada especie para dibujar.
# Se añade una variable nueva con los colores
color <- rep("green",nrow(datos.entreno))
color[datos.entreno$Species == "setosa"] <- "red"
color[datos.entreno$Species == "virginica"] <- "blue"

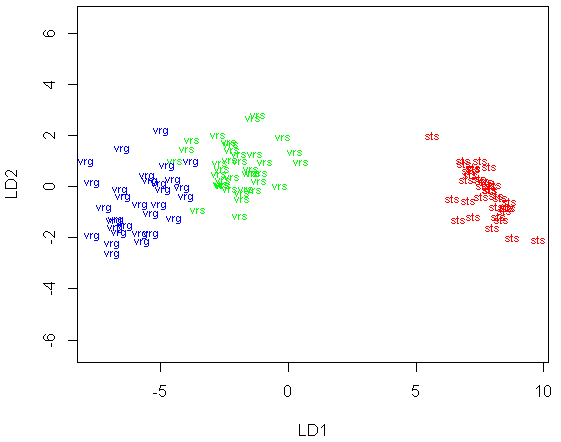
# Gráficos de las 2 primeras componentes del AD lineal.
# Abbrev abrevia los nombres
plot(datos.entreno.lda, dimen=2, col=color, abbrev=3)

# pairs() Dibuja los pares de componentes.
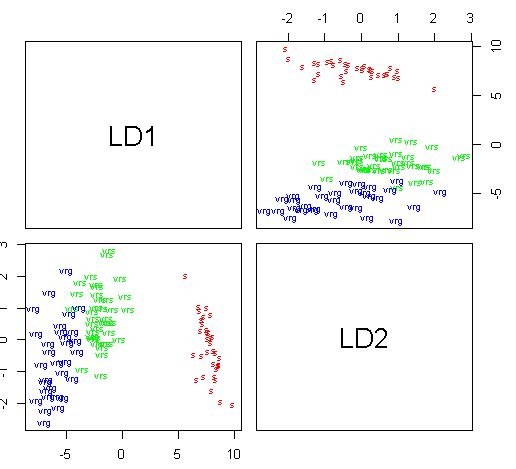
# En este ejemplo no tiene mucho sentido ya que sólo hay 2.
# Las componentes son el número de clases menos 1
pairs(datos.entreno.lda, col=color, abbrev=1)

# Matriz de confusión:
mc <- table(datos.entreno.lda.p$class, datos.test$Species)
mc

##             
##              setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         12         0
##   virginica       0          0        18

# Correctamente clasificados en %
100 * sum(diag(mc)) / sum(mc)

## [1] 100

# predicción. Se asignan valores nuevos a cada variable
nuevo <- data.frame(Sepal.Length=5, Sepal.Width=3, Petal.Length=1.5, Petal.Width=0.3)
prediccion <- predict(datos.entreno.lda,newdata=nuevo, interval='confidence')

# Nos devuelve a la que ha asignado la predicción
prediccion$class

## [1] setosa
## Levels: setosa versicolor virginica

# Probabilidad de pertenencia a cada clase:
prediccion$posterior

##   setosa   versicolor    virginica
## 1      1 4.782878e-17 1.421194e-35