Definición de función de coste
La función de coste trata de determinar el error entre el valor estimado y el valor real, con el fin de optimizar los parámetros de la red neuronal.
Estimadores de error de la función de coste
Raíz cuadrada media – RMSE
La raíz cuadrada media, es una medida de precisión calculada como la raíz cuadrada media de los residuos. Se entiende como residuos la diferencia entre el valor previsto (correcto) y el valor real obtenido.
Raíz cuadrada media
Características del RMSE:
- Penaliza los valores que son muy grandes.
- No es fácilmente interpretable.
- Funciona muy bien para optimizar regresiones en general.
Error absoluto medio – MAE
El error absoluto medio, es una medida de precisión y se calcula como la suma media de los valores absolutos de los errores.
Error absoluto medio
Características del MAE:
- Más difícil diferenciación y convergencia.
- Penaliza menos los valores grandes
- Es más fácil de interpretar
Error absoluto medio escalado – MASE
El error absoluto medio escalado, es una medida de precisión similar al MAE pero escalado.
Error absoluto medio escalado
Características del MASE:
- Más difícil diferenciación y convergencia.
- Escala univariante.
- Simétrica.
- Es más fácil de interpretar.
Entropía cruzada categórica – Categorical Cross-Entropy
La entropía cruzada categórica, es una medida de precisión para variables categóricas.
Entropía cruzada categórica
Características del Entropía cruzada categórica:
- Más difícil diferenciación y convergencia.
- Escala univariante.
- Simétrica.
- Es más fácil de interpretar.
Entropía cruzada binaria – Binary Cross-Entropy
La entropía cruzada binaria, es una medida de precisión para variables binarias.
Entropía cruzada binaria
Características del Entropía cruzada binaria:
- Más difícil diferenciación y convergencia.
- Escala univariante.
- Simétrica.
- Es más fácil de interpretar.
Tipos de optimizadores de la función de coste.
Descenso estocástico del gradiente – SGD (Stochastic Gradient Descent)
Adam
El optimizador Adam trata de solventar el problema con la fijación de el ratio de aprendizaje del SGD, para ello adapta el ratio de aprendizaje en función de cómo estén distribuidos los parámetros. Si los parámetros están muy dispersos (sparse) el ratio de aprendizaje aumentará.
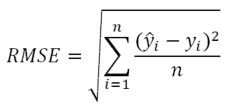
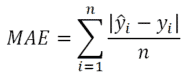
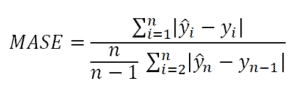
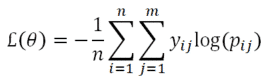
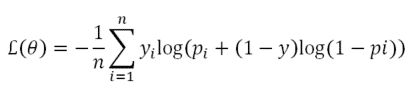
No tengo experiencoa. Por favor, ¿cómo escribo esa notación matemática en un programa de Pyhon, por ejemplo, para poder calcular?
*experiencia