Uso: Clasificador lineal.

Descripción: El análisis de la regresión es una técnica estadística para estimar las relaciones que existen entre variables.

En este modelo se fija la variable que se quiere predecir (variable dependiente) y se determina la relación con el resto de variables predictoras (independientes)

En la regresión lineal múltiple existe más de una variable independiente que predice el comportamiento de la variable dependiente.

Variable dependiente: Métrica.

Variables independientes: Métricas y/o no métricas.

Ejemplo en R: Determinar el tiempo necesario para organizar diferentes bloques de cajas que se encuentran a diferentes distancias.

# Carga de datos
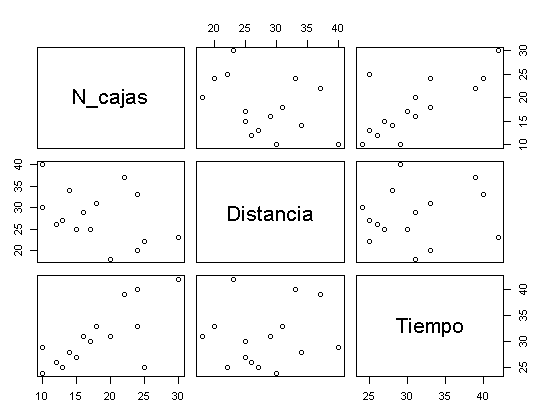
 datos <- read.table("https://www.diegocalvo.es/wp-content/uploads/2016/09/datos-regresion-lineal-multiple.txt", header = TRUE)

# Explorar la relación entre todas las parejas de variables
pairs(datos)

# Calcular la intensidad de la relación mediante un análisis de correlación.
cor(datos)

             N_cajas  Distancia    Tiempo
N_cajas    1.0000000 -0.4052976 0.7246466
Distancia -0.4052976  1.0000000 0.1269032
Tiempo     0.7246466  0.1269032 1.0000000

# Mostramos visualmente la relación de la variable dependiente con cada una de las variables independientes
plot(datos$Tiempo,datos$N_cajas)
plot(datos$Tiempo,datos$Distancia)

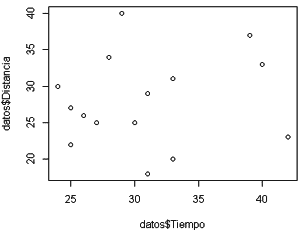
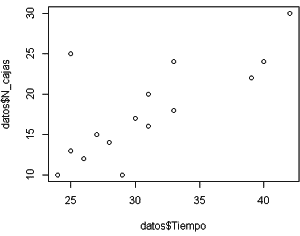
# A partir de los análisis realizados se opta por realizar un modelo múltiple lineal del tipo y = ax1 + bx2 + c

modelo1<- lm(datos$Tiempo~datos$N_cajas+datos$Distancia, data=datos)
summary(modelo1)

Call:
lm(formula = datos$Tiempo ~ datos$N_cajas + datos$Distancia, 
    data = datos)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.2716 -0.5405  0.5212  1.4051  2.9381 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)       2.3112     5.8573   0.395  0.70007    
datos$N_cajas     0.8772     0.1530   5.732 9.43e-05 ***
datos$Distancia   0.4559     0.1468   3.107  0.00908 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.141 on 12 degrees of freedom
Multiple R-squared:  0.7368,	Adjusted R-squared:  0.6929 
F-statistic:  16.8 on 2 and 12 DF,  p-value: 0.0003325

# A partir de esta análisis deducimos que el modelo queda: Tiempo = 0,8772*N_cajas + 0,4559*Distancia + 2,3112 + error
formula(modelo1)

# Fijándonos en R cuadrado (0,7368) vemos que el modelo no estima con precisión y vamos a probar a eliminar una variable para ver si mejora su precisión.

# Nuevo modelo: Tiempo  = a*N_cajas + b + error

modelo2 <- lm(datos$Tiempo~datos$N_cajas, data=datos)
summary(modelo2)

Call:
lm(formula = datos$Tiempo ~ datos$N_cajas, data = datos)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.6583  -1.6018  -0.1821   2.5262   5.3952 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)    18.5452     3.4142   5.432 0.000115 ***
datos$N_cajas   0.6845     0.1805   3.791 0.002244 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.053 on 13 degrees of freedom
Multiple R-squared:  0.5251,	Adjusted R-squared:  0.4886 
F-statistic: 14.37 on 1 and 13 DF,  p-value: 0.002244

# Analizados los dos modelos vemos que el modelo primero ajusta mejor que el segundo
# Para comparar ambos modelos se recurre al análisis ANOVA
anova(modelo2,modelo1)

Analysis of Variance Table

Model 1: datos$Tiempo ~ datos$N_cajas
Model 2: datos$Tiempo ~ datos$N_cajas + datos$Distancia
  Res.Df    RSS Df Sum of Sq      F   Pr(>F)   
1     13 213.57                                
2     12 118.38  1    95.198 9.6505 0.009079 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

# Viendo el resultado podemos concluir que el modelo que mejor se ajusta es el modelo más complejo = modelo1

# Para que este modelo sea fiable debemos realizar un ANALISIS DE RESIDUOS

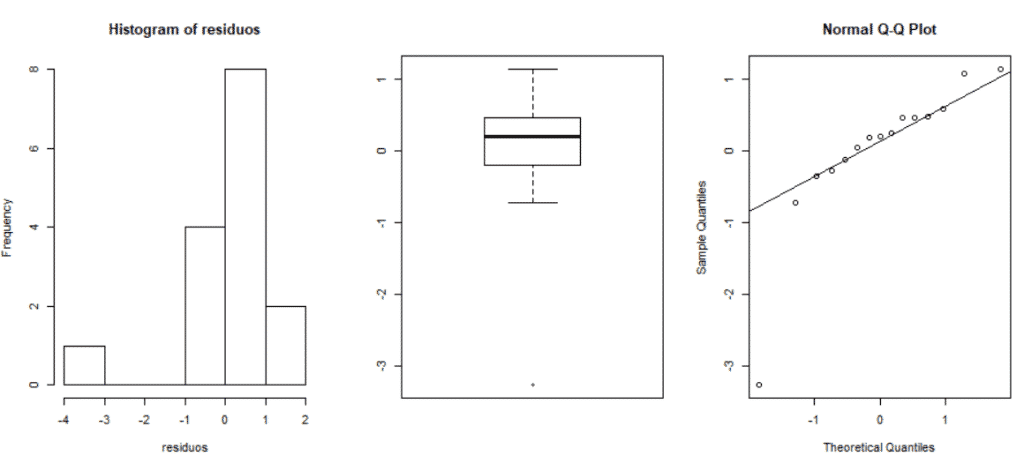
# SUPUESTO 1: Los errores deben seguir una distribución normal

residuos<-rstandard(modelo1) # residuos estándares del modelo ajustado (completo) 
win.graph() # abre una ventana para los gráficos 
par(mfrow=c(1,3)) # divide la ventana en una fila y tres columnas 
hist(residuos) # histograma de los residuos estandarizados 
boxplot(residuos) # diagrama de cajas de los residuos estandarizados 
qqnorm(residuos) # gráfico de cuantiles de los residuos estandarizados 
qqline(residuos)

Estudio de los residuos

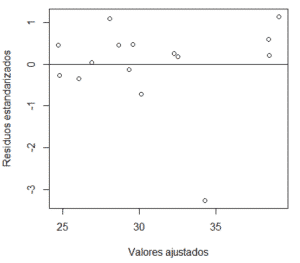
# SUPUESTO 2: La varianza de los errores  es constante

plot(fitted.values(modelo1),rstandard(modelo1), xlab="Valores ajustados", ylab="Residuos estandarizados")  # gráfico 2D de los valores ajustados vs. los residuos estandarizados 
abline(h=0) # dibuja la recta en cero

Estudio de la varianza de los errores

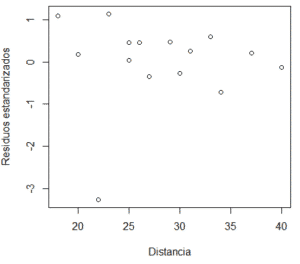
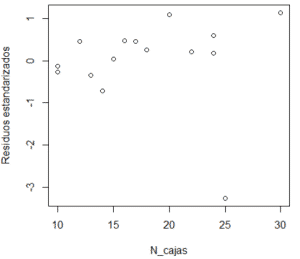
# SUPUESTO 3: La independencia de los errores

plot(datos$N_cajas,rstandard(modelo1),xlab="N_cajas",ylab="Residuos estandarizados") 
plot(datos$Distancia,rstandard(modelo1),xlab="Distancia",ylab="Residuos estandarizados")