Se va a exponer el análisis que se realizó antes del partido Espanyol-Barcelona, el cual se jugo el 8/7/2020, de manera que se puedan obtener las probabilidades que existen, basándonos en un histórico de partidos y de datos, de acertar ciertos mercados que nos ofrecen las casas de apuestas, en este caso nos centraremos en el mercado de que haya cierta cantidad de amarillas en el partido, de que se produzca un cierto resultado y de que se metan una cierta cantidad de goles.

Se llevará a cabo mediante Rstudio apoyándonos en el motor de procesamiento de datos Apache Spark.

1. Instalación y carga de paquetes

Se instalarán y cargarán las librerías que necesitamos.

install.packages(c("readxl", "dplyr"))
install.packages("tidyverse")
install.packages("sparklyr")

library(readxl)
library(dplyr)
library(tidyverse)
library(sparklyr)

spark_install("3.0.0")#Instalación de spark

sesion_spark <- spark_connect(master="local", version="3.0.0")#Conexión con spark desde local

2. Carga de datos

Cargamos los datos pertenecientes a los partidos históricos entre el Barcelona y Espanyol, así como los datos pertenecientes a los partidos jugados por el Espanyol en las 3 últimas temporadas.

Podemos descargar el archivo con los datos a continuación.

Resultados <- read_excel("Datos espanyol históricos.xlsx", sheet = "Resultados 3 años")
Rivales <- read_excel("Datos espanyol históricos.xlsx", sheet = "Rival ult año")
Arbitros <- read_excel("Datos espanyol históricos.xlsx", sheet = "Arbitros 3 años")
Part_Barcelona <- read_excel("Datos espanyol históricos.xlsx", sheet = "Partidos contra el barcelona")
Result_Barcelona <- read_excel("Datos espanyol históricos.xlsx", sheet = "Resultados contra el barcelona")
Arbitros_Barcelona <- read_excel("Datos espanyol históricos.xlsx", sheet = "Arbitros vs Barcelona")

3. Operaciones con datos

Vamos a renombrar las columnas de los Dataframes cargados desde el archivo Excel, de forma que las columnas de cada Dataframe quede mejor definida.

colnames(Arbitros) <- c("Arbitro","Partidos_jugados","Partidos_ganados","Partidos_empatados","Partidos_perdidos","Goles_favor","Goles_contra","Tarjetas_amarillas","Tarjetas_rojas","Temporada")

colnames(Arbitros_Barcelona) <- c("Arbitro","Partidos_jugados","Partidos_ganados","Partidos_empatados","Partidos_perdidos","Goles_favor","Goles_contra","Tarjetas_amarillas","Tarjetas_rojas")

colnames(Part_Barcelona) <- c("Temporada","Partidos_jugados","Partidos_ganados","Partidos_empatados","Partidos_perdidos","Goles_favor","Goles_contra","Tarjetas_amarillas","Tarjetas_rojas","Tipo")

colnames(Rivales) <- c("Nombre","Partidos_jugados","Partidos_ganados","Partidos_empatados","Partidos_perdidos","Goles_favor","Goles_contra","Tarjetas_amarillas","Tarjetas_rojas","Temporada","Tipo")

4. Análisis de datos

Queremos analizar el mercado de tarjetas amarillas, por ello vamos a analizar estos 4 dataframes: Arbitros_Barcelona, Rivales, Arbitros, Part_Barcelona.

4.1 Análisis mercado de tarjetas amarillas

En primer lugar analizamos las amarillas del Dataframe Part_Barcelona que se corresponde con los partidos jugados del Espanyol frente al Barcelona.

#Vamos a obtener un histograma por rangos que nos diga el número de tarjetas amarillas sacadas a los jugadores del espanyol en los partidos históricos entre Barcelona y espanyol

qplot(Tarjetas_amarillas, data=Part_Barcelona,
      geom="histogram",
      binwidth = 1,  
      xlab = "Tarjetas amarillas",  
      fill=I("blue"), 
      col=I("red"), 
      alpha=I(.2)
      )+
  theme_minimal()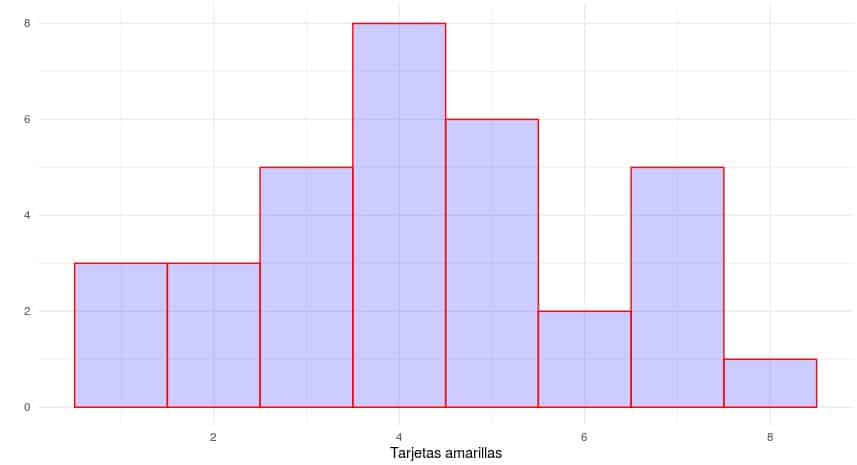

Nos centramos en un mercado en concreto, por ejemplo, en el mercado de más de 3 amarillas al espanyol.

El primer análisis que hacemos es calcular la probabilidad de en cuantos partidos contra el Barcelona hubo más de 3 tarjetas sacadas al Espanyol.

Part_Barcelona2 <- sdf_copy_to(sesion_spark,Part_Barcelona) #Copiamos la variable a Spark

  Mc <- Part_Barcelona2 %>%
    ft_binarizer(
    input_col = "Tarjetas_amarillas",
    output_col= "Mas_de_3",
    threshold= 3
  )%>%
  group_by(Mas_de_3)%>%
  tally()%>%
  arrange(Mas_de_3)%>%
  collect()

#Calculamos el porcentaje de partidos en los que ocurre 
Mc[2,2]/sum(Mc$n)*100 

##          n
## 1 66.66667

Observamos que ocurre en un 66,66% de los partidos.

Si quisiéramos saber en cuantos hay más de 4 tarjetas siendo un poco más restrictivos

Mc2 <- Part_Barcelona2 %>%
  ft_binarizer(
    input_col = "Tarjetas_amarillas",
    output_col= "Mas_de_4",
    threshold= 4
  )%>%
  group_by(Mas_de_4)%>%
  tally()%>%
  arrange(Mas_de_4)%>%
  collect()

Mc2[2,2]/sum(Mc2$n)*100 

##          n
## 1 42.42424

Observamos que ocurre en un 42,42% de los partidos.

Vamos con el siguiente análisis de datos, ahora se van a analizar los partidos con los rivales de la ultima temporada.

En primer lugar, analizamos el mercado de mas de 3 tarjetas amarillas.

Rivales2<- sdf_copy_to(sesion_spark,Rivales) #Copiamos la variable a Spark

Mc3 <- Rivales2 %>%
  ft_binarizer(
    input_col = "Tarjetas_amarillas",
    output_col= "Mas_de_3",
    threshold= 3
  )%>%
  group_by(Mas_de_3)%>%
  tally()%>%
  arrange(Mas_de_3)%>%
  collect()

Mc3[2,2]/sum(Mc3$n)*100 

##          n
## 1 26.47059

Observamos que ocurre en un 26,47% de los partidos.

Analizamos el mercado de mas de 4 tarjetas amarillas

Mc4 <- Rivales2 %>%
  ft_binarizer(
    input_col = "Tarjetas_amarillas",
    output_col= "Mas_de_4",
    threshold= 4
  )%>%
  group_by(Mas_de_4)%>%
  tally()%>%
  arrange(Mas_de_4)%>%
  collect()

Mc4[2,2]/sum(Mc4$n)*100 

##          n
## 1 8.823529

Observamos que ocurre en un 8.82% de los partidos.

Vamos ahora a analizar a los árbitros, empezamos analizando cuantas tarjetas ha sacado Munuera Montero J., el cual es el arbitro del partido Barcelona-Espanyol del 8/7/2020, en los partidos históricos contra el Barcelona.

filter(Arbitros_Barcelona, Arbitro="Munuera Montero")

## Error: Problem with `filter()` input `..1`.
## x Input `..1` is named.
## ℹ This usually means that you've used `=` instead of `==`.
## ℹ Did you mean `Arbitro == "Munuera Montero"`?
## Run `rlang::last_error()` to see where the error occurred.

Podemos observar que aparece un error, eso significa que no cuentra el texto y por tanto, nunca ha arbitrado Munuera Montero un partido entre Barcelona y Espanyol.

Vamos a analizar a Munuera Montero en los partidos que ha arbitrado al Espanyol en las 3 ultimas temporadas.

Arbitros_Munuera <- filter(Arbitros, Arbitro=='Munuera Montero')

Arbitros_Munuera2 <- select(Arbitros_Munuera, Arbitro,Partidos_jugados, Tarjetas_amarillas)

head(Arbitros_Munuera2)

##   Arbitro         Partidos_jugados Tarjetas_amarillas
##   <chr>                      <dbl>              <dbl>
## 1 Munuera Montero                3                  6
## 2 Munuera Montero                2                  3
## 3 Munuera Montero                1                  2

sum(Arbitros_Munuera2$Tarjetas_amarillas)

## [1] 11

Ha sacado un total de 11 amarillas en 9 encuentros del espanyol, por tanto podemos destacar que este árbitro no saca muchas amarillas cuando interviene el espanyol.

4.2 Análisis mercado de resultado exacto

Ahora vamos a actuar en otro mercado que es el del resultado exacto que pueda ocurrir en el partido. Para ello analizamos los Resultados con el Barcelona históricos y los Resultados de la última campaña.

Primero empezamos con los partidos entre Espanyol y Barcelona históricos

#Se observa los resultados más repetidos del enfrentamiento Barcelona-Espanyol o Espanyol-Barcelona

Resultados_esp_bar <- aggregate(Número ~ Resultado, FUN = sum, data = Result_Barcelona)
Resultados_esp_bar  <- arrange(Resultados_esp_bar , desc(Número))
Resultados_esp_bar 

Se observa que el resultado 1-0 es el más repetido

Calculamos la probabilidad de que suceda el 1-0 como factor más repetitivo

(max(Resultados_esp_bar $Número)/sum(Resultados_esp_bar $Número))*100

## [1] 11.11111

Observamos que ocurre en un 11,11% de los partidos

Analizamos también el segundo resultado más repetido 1-1.

((Resultados_esp_bar [2,2])/sum(Resultados_esp_bar $Número))*100

## [1] 10.52632

Observamos que ocurre en un 10.52% de los partidos

Vamos a ver ahora el resultado más repetido cuando el Espanyol juega de visitante

Resultados_vis <- Result_Barcelona %>%
  group_by(Resultado)%>%
  filter(Tipo=='Visitante')%>%
  arrange(desc(Número))%>%
  collect

Resultados_vis

Se observa que el resultado más repetido cuando el Espanyol juega de visitante es el 1-0, es decir, 1-0 a favor del Barcelona

Calculamos la probabilidad de que suceda el 1-0 como factor más repetitivo

(max(Resultados_vis$Número)/sum(Resultados_vis$Número))*100

## [1] 16.47059

Observamos que ocurre en un 16.47% de los partidos

Analizamos el 1-1 ya que es un resultado con mucha relevancia en los otros análisis.

((Resultados_vis[8,3])/sum(Resultados_vis$Número))*100

## [1] 3.529412

Observamos que ocurre en un 3.52% de los partidos

Ahora analizamos los resultados de la ultima temporada del Espanyol

#Se observa los resultados más repetidos de los enfrentamientos del Espanyol estas 3 últimas temporadas.

Resultados2 <- aggregate(Partidos ~ Resultado, FUN = sum, data = Resultados)
Resultados2 <- arrange(Resultados2, desc(Partidos))
Resultados2

Para este caso tenemos que el resultado mas repetitivo para el Espanyol en sus partidos es el 1-1, independientemente de juegue como Local o visitante

Vamos a calcular la probabilidad de que suceda este Resultado

(max(Resultados2$Partidos)/sum(Resultados2$Partidos))*100

## [1] 16.36364

Observamos que ocurre en un 16.36% de los partidos

Se van a calcular las probabilidades de que el partido acabe 1-0 dado que era el resultado también más repetido en los enfrentamientos frente al Barcelona, tanto en el computo general como cuando jugaba de visitante.

(Resultados2[2,2]/sum(Resultados2$Partidos))*100

## [1] 14.54545

Observamos que ocurre en un 14.54% de los partidos

Vamos a ver ahora el resultado más repetido cuando el Espanyol juega de visitante

Resultados2_vis <- Resultados %>%
  group_by(Resultado)%>%
  filter(Tipo=='Visitante')%>%
  arrange(desc(Partidos))%>%
  collect

Resultados2_vis_fin <- aggregate(Partidos ~ Resultado, FUN = sum, data = Resultados2_vis)
Resultados2_vis_fin <- arrange(Resultados2_vis_fin , desc(Partidos))
Resultados2_vis_fin

Se observa que el resultado más repetido cuando el Espanyol juega de visitante es el 1-1

Calculamos la probabilidad de que suceda el 1-1 como factor más repetitivo

(max(Resultados2_vis_fin$Partidos)/sum(Resultados2_vis_fin$Partidos))*100

## [1] 14.54545

Observamos que ocurre en un 14.54% de los partidos

Calculamos también la probabilidad de que suceda el 1-0, el cual es el segundo resultado más repetido.

((Resultados2_vis_fin[2,2])/sum(Resultados2_vis_fin$Partidos))*100

## [1] 12.72727

Observamos que ocurre en un 12.72% de los partidos

También podemos hacer un análisis de goles según el arbitro del encuentro, que en este caso será Munuera Montero.
En este caso el análisis será de las ultimas tres temporadas.

Arbitros_Munuera <- filter(Arbitros, Arbitro=='Munuera Montero')

Arbitros_Munuera_goles <- select(Arbitros_Munuera, Arbitro,Partidos_jugados, Goles_favor, Goles_contra)

Goles_favor <- aggregate(Goles_favor ~ Arbitro, FUN = sum, data = Arbitros_Munuera_goles)

Goles_contra <- aggregate(Goles_contra ~ Arbitro, FUN = sum, data = Arbitros_Munuera_goles)

Part_jug_Munuera <- aggregate(Partidos_jugados ~ Arbitro, FUN = sum, data = Arbitros_Munuera_goles)

Estadist_Munuera <- data.frame(Arbitro=Goles_favor$Arbitro, Goles_a_favor=Goles_favor$Goles_favor, Goles_en_contra=Goles_contra$Goles_contra, Partidos_jugados=Part_jug_Munuera$Partidos_jugados)

Estadist_Munuera

##          Arbitro Goles_a_favor Goles_en_contra Partidos_jugados
## 1 Munuera Montero             7               1                6

Se han metido un total de 7 goles a favor del espanyol y 1 gol en contra en los 6 partidos de las ultimas 3 temporadas en los que participaba Munuera Montero.

En este caso habría que entrar a analizar contra que equipos han sido esos partidos y más variables de interés, es por tanto que este dato es el que menos relevancia tiene entre todos los análisis realizados.

4.3 Análisis mercado de goles en el partido

Por último vamos a realizar un análisis del mercado de goles del partido.

#Volvemos a atender a los resultados más repetidos de los Barcelona-Espanyol

Resultados_esp_bar

Vamos a fijarnos como objetivo analizar el mercado de que probabilidad hay de que se marque 1 gol o más, para ello vamos a eliminar los resultados que sean 0-0.

(sum(Resultados_esp_bar$Número)-Resultados_esp_bar[4,2])/(sum(Resultados_esp_bar$Número))*100

## [1] 92.98246

Observamos que ocurre en un 92.98% de los partidos

Analizamos ahora las probabilidades atendiendo al histórico entre Barcelona y Espanyol cuando el Espanyol es visitante.

Resultados_vis

(sum(Resultados_vis$Número)-Resultados_vis[9,3])/(sum(Resultados_vis$Número))*100

##     Número
## 1 96.47059

Observamos que ocurre en un 96.47% de los partidos

Vamos a analizar ahora los partidos jugados estas 3 últimas temporadas

Queremos obtener la probabilidad de que se marque al menos 1 gol

Resultados2

((sum(Resultados2$Partidos)-Resultados2[7,2])/sum(Resultados2$Partidos))*100

## [1] 93.63636

Observamos que ocurre en un 93.63% de los partidos

Ahora analizamos cuando juega de visitante

Resultados2_vis_fin

(sum(Resultados2_vis_fin$Partidos)-Resultados2_vis_fin[4,2])/(sum(Resultados2_vis_fin$Partidos))*100

## [1] 90.90909

Observamos que ocurre en un 90.90% de los partidos

Si quisieramos ser más restrictivos con nuestra apuesta y ver que probabilidad hay de que se marquen al menos 2 goles

Analizamos para el histórico de partidos entre espanyol y barcelona

Debemos eliminar todos los resultados donde haya 1 gol o menos, es decir, 0-0, 1-0 o 0-1.

Resultados_esp_bar

Mercado_2goles <- Resultados_esp_bar[-c(1, 4, 5), ] 

(sum(Mercado_2goles$Número))/(sum(Resultados_esp_bar$Número))*100

## [1] 76.02339

Observamos que ocurre en un 76.02% de los partidos

Si lo hacemos para cuando el espanyol juega de visitante

Resultados_vis

Mercado_2goles_vis <- Resultados_vis[-c(1, 9, 13), ] 

(sum(Mercado_2goles_vis$Número))/(sum(Resultados_vis$Número))*100

## [1] 77.64706

Observamos que ocurre en un 77,64% de los partidos

Vamos a analizar ahora los partidos jugados estas 3 últimas temporadas

Resultados2

Mercado_2goles2 <- Resultados2[-c(2, 3, 7), ]

((sum(Mercado_2goles2$Partidos))/sum(Resultados2$Partidos))*100

## [1] 70

Observamos que ocurre en un 70% de los partidos

Por último, analizamos cuando el Espanyol juega de visitante

Resultados2_vis_fin

Mercado_2goles2_vis <- Resultados2_vis_fin[-c(2, 4, 9), ]

(sum(Mercado_2goles2_vis$Partidos))/(sum(Resultados2_vis_fin$Partidos))*100

## [1] 72.72727

Observamos que ocurre en un 72,72% de los partidos

5. Conclusiones

Una vez finalizado el partido observamos los resultados que se dieron y las probabilidades que teníamos de que sucedieran los eventos determinados

5.1 Mercado de tarjetas amarillas al espanyol:

Se realizará un análisis de las probabilidades obtenidos en función a cada conjunto de datos

• Probabilidad de sacarse más de 3 tarjetas amarillas en función al histórico entre Barcelona y Espanyol: 66,66%

• Probabilidad de sacarse más de 3 tarjetas amarillas en función a la última temporada: 26,47%

• Probabilidad de sacarse más de 4 tarjetas amarillas en función al histórico entre Barcelona y Espanyol: 42,42%

• Probabilidad de sacarse más de 4 tarjetas amarillas en función a la última temporada: 8,82%

Si hicieramos una probabilidad compuesta de las probabilidades más relevantes de cada mercado para obtener la predicción obtendriamos lo siguiente, suponemos un peso un poco mayor a las probabilidades de la última temporada (0,6):

• Probabilidad de que se saquen más de 3 amarillas al espanyol: 66,66% * 0,4 + 26,47% * 0,6= 42,54%

• Probabilidad de que se saquen más de 4 amarillas al espanyol: 42,42% * 0,4 + 8,82 * 0,6= 22,26%

¿Qué paso en el partido?

Se sacaron 3 amarillas al Espanyol, por tanto de haber apostado a este mercado, la apuesta habría sido baja debido a que sucede con un 42,54% de probabilidad, es decir, en menos de 1 de cada 2 partidos.

5.2 Mercado de resultado exacto

Se analizarán los resultados con mayor probabilidad en los análisis, es decir, 1-0 y 1-1:

• Probabilidad de que haya un 1-0 en función al histórico entre Barcelona y Espanyol : 11,11%

• Probabilidad de que haya un 1-0 en función al histórico Barcelona-Espanyol (jugando de visitante): 16,47%

• Probabilidad de que haya un 1-0 en función a las 3 últimas temporadas: 14,54%

• Probabilidad de que haya un 1-0 en función a las 3 últimas temporadas (jugando como visitante): 12,72%

• Probabilidad de que haya un 1-1 en función al histórico entre Barcelona y Espanyol : 10,52%

• Probabilidad de que haya un 1-1 en función al histórico Barcelona-Espanyol (jugando de visitante): 3,52%

• Probabilidad de que haya un 1-1 en función a las 3 últimas temporadas: 16,36%

• Probabilidad de que haya un 1-1 en función a las 3 últimas temporadas (jugando como visitante): 14,54%

Si hicieramos una probabilidad compuesta de las probabilidades más relevantes de cada mercado para obtener la predicción obtendriamos lo siguiente, suponemos un peso un poco mayor a las probabilidades de las últimas temporadas (0,3) y un poco menor a las probabilidades históricas (0,2):

• Probabilidad de un 1-0 en el partido: 13,7%

• Probabilidad de un 1-1 en el partido: 12,07%

¿Qué paso en el partido?

1-0 fue el resultado final, por tanto de haber apostado a este mercado, aunque la apuesta habría sido baja debido a que sucede con un 13,07% de probabilidad, habríamos acertado, y estos mercados se suelen pagar a cuota muy alta.

5.3 Mercado de goles en el partido

Se analizarán las probabilidades de marcarse un gol en base al histórico de datos:

• Probabilidad de marcarse al menos 1 gol en función al histórico entre Barcelona y Espanyol: 92.98%

• Probabilidad de marcarse al menos 1 gol en función al histórico Barcelona-Espanyoljugando como visitante: 96,47%

• Probabilidad de marcarse al menos 1 gol en función a las 3 últimas temporadas: 93,63%

• Probabilidad de marcarse al menos 1 gol en función a las 3 últimas temporadas (jugando como visitante): 90,90%

• Probabilidad de marcarse al menos 2 goles en función al histórico entre Barcelona y Espanyol: 76,02%

• Probabilidad de marcarse al menos 2 goles en función al histórico Barcelona-Espanyoljugando como visitante: 77,64%

• Probabilidad de marcarse al menos 2 goles en función a las 3 últimas temporadas: 70%

• Probabilidad de marcarse al menos 2 goles en función a las 3 últimas temporadas (jugando como visitante): 72,72%

Si hicieramos una probabilidad compuesta de las probabilidades más relevantes de cada mercado para obtener la predicción obtendriamos lo siguiente, suponemos un peso un poco mayor a las probabilidades de las últimas temporadas (0,3) y un poco menor a las probabilidades históricas (0,2):

• Probabilidad de marcarse al menos 1 gol: 93,24%

• Probabilidad de marcarse al menos 2 goles: 73,55%

¿Qué paso en el partido?

Se marcó 1 gol en el partido, por tanto de haber apostado al mercado de al menos 1 gol habríamos acertado, la probabilidad de que esto sucediera estaba muy a favor dado que pasaba con una probabilidad de 93,24%.