El objetivo de este modelo será predecir que calificación obtendrá una película en función de su presupuesto y de su duración

Se va a usar el paquete de ggplot2movies, el cual almacena una serie de películas así como una serie de variables que las caracterizan.

Instalación y carga de paquetes

#Instalación de paquetes
install.packages("ggplot2movies")
install.packages("ggplot2") 
install.packages("tidyverse")
install.packages("dplyr") 

#Carga de paquetes
library(ggplot2movies)
library(ggplot2) 
library(tidyverse)
library(dplyr) 

Tratamiento de datos

En primer lugar, asignamos el dataframe movies del paquete ggplot2movies, a la variable peliculas y después eliminamos las filas que tengan datos nulos

peliculas <- movies 

pelis_presupuesto <- na.omit(peliculas)

Ahora seleccionamos las variables que nos interesan, las cuales son rating como variable que queremos predecir y como variables independientes length y budget, es decir, duración y presupuesto.

peliculas.ML_presupuesto <- select(pelis_presupuesto, length, budget, rating)

Ahora vamos a ver la correlación que existe entre las variables

cor(peliculas.ML_presupuesto)

##            length      budget      rating
## length 1.00000000  0.33818503  0.02836237
## budget 0.33818503  1.00000000 -0.01422905
## rating 0.02836237 -0.01422905  1.00000000

Observamos que existe una correlación entre la duración y el presupuesto de las películas, con esto habrá que tener cuidado a la hora de realizar la modelización.

Observamos con gráficas las relaciones de variables.

ggplot(peliculas.ML_presupuesto, aes(x = rating, y = length)) +
  geom_point( size=2 ) + 
  theme_minimal() +
  xlab("Calificaciones") +
  ylab("Duración")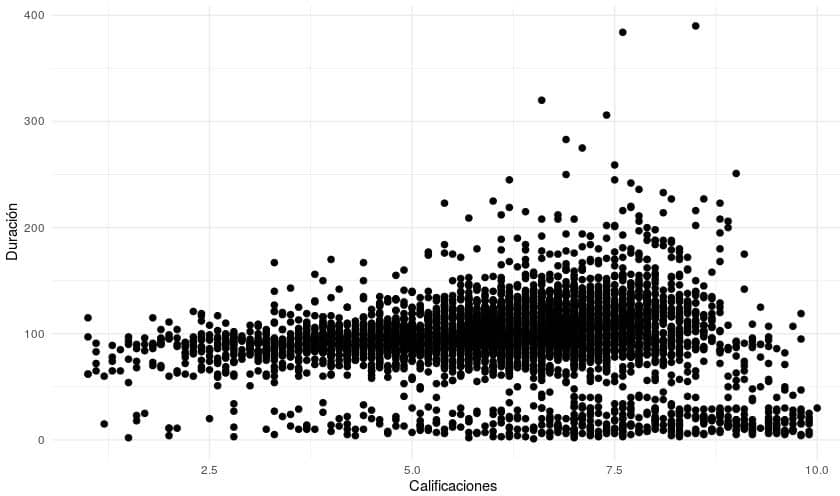

ggplot(peliculas.ML_presupuesto, aes(x = rating, y = budget)) +
  geom_point( size=2 ) + 
  theme_minimal() +
  xlab("Calificaciones") +
  ylab("Presupuesto")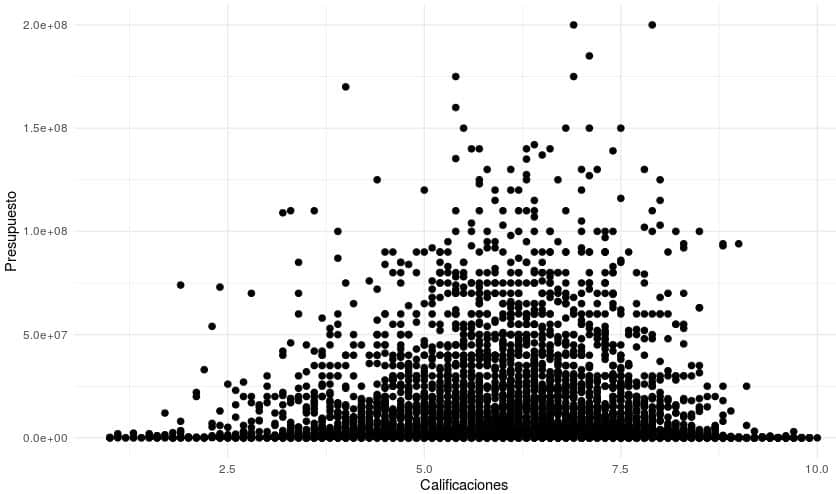

Se observa que hay muchas películas que no afectan a nuestro modelo por sus características (presupuestos muy bajos o duraciones muy bajas)

Vamos ahora a agrupar las películas por año de estreno para seguir encontrando patrones raros

peliculas %>%
  mutate(year=as.character(year))%>%
  group_by(year)%>%
  tally()

## A tibble: 113 x 2
##   year      n
##   <chr> <int>
## 1 1893      1
## 2 1894      9
## 3 1895      3
## 4 1896     13
## 5 1897      9
## 6 1898      5
## 7 1899      9
## 8 1900     16
## 9 1901     28
##10 1902      9
## … with 103 more rows

Se observa que existen películas muy antiguas que puede que no guarden el mismo patrón que las películas actuales, condición que confirma la anterior suposición.

Por tanto, vamos a quedarnos con las películas que tengan una duración mayor a 75 pero no mayor de 200 y con un presupuesto mayor a 5000000

Peliculas_modelo <- filter(peliculas.ML_presupuesto, length>=75, budget >= 5000000) # AND Lógico
Peliculas_modelo <- filter(peliculas.ML_presupuesto, length<=200, budget >= 5000000) # AND Lógico

Comprobamos las gráficas de nuevo

ggplot(Peliculas_modelo, aes(x = rating, y = length)) +
  geom_point( size=2 ) + 
  theme_minimal() +
  xlab("Calificaciones") +
  ylab("Duración")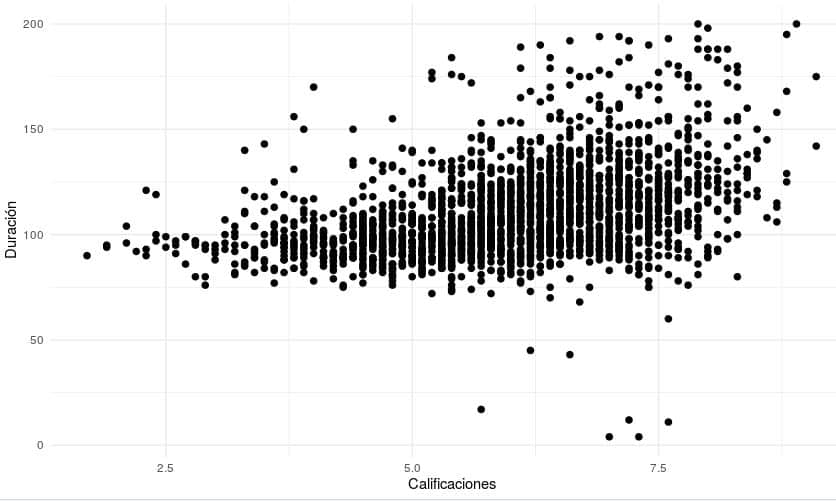

ggplot(Peliculas_modelo, aes(x = rating, y = budget)) +
  geom_point( size=2 ) + 
  theme_minimal() +
  xlab("Calificaciones") +
  ylab("Presupuesto")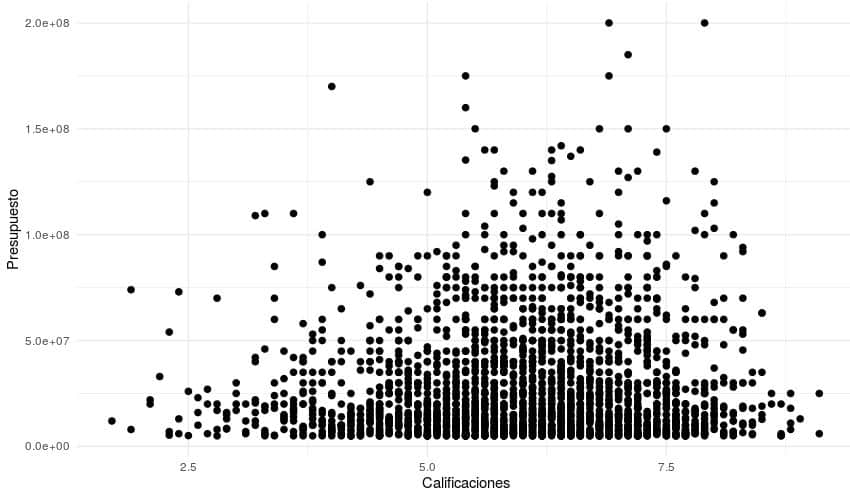

Se puede observar que hemos eliminado muchos de los puntos con patrones raros por tratarse de películas antiguas, con duración muy baja y/o con presupuesto muy bajo.

Modelización

Vamos ahora con la modelización de los datos mediante una regresión lineal múltiple dado que se requerirá de varias variables para predecir una variable dependiente numérica.

#En primer lugar, tomamos en consideración el presupuesto y la duración 
modelo1<- lm(rating~budget+length, data=Peliculas_modelo)
summary(modelo1)

## Call:
## lm(formula = rating ~ budget + length, data = Peliculas_modelo)

## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.9298 -0.6926  0.0439  0.7674  3.8491 

## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3.503e+00  1.237e-01  28.311   <2e-16 ***
## budget      -1.392e-09  8.674e-10  -1.604    0.109    
## length       2.316e-02  1.116e-03  20.749   <2e-16 ***
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

## Residual standard error: 1.124 on 2196 degrees of freedom
## Multiple R-squared:  0.1655,	Adjusted R-squared:  0.1648 
## F-statistic: 217.8 on 2 and 2196 DF,  p-value: < 2.2e-16

#Vamos a eliminar algun factor como el budget de la formula dado que como podemos observar no tiene ningún asterisco, lo cual significa que no contribuye con tanta relevancia en la predicción de la variable dependiente.

#De forma que ahora usaremos una regresión lineal simple

modelo2<- lm(rating~length, data=Peliculas_modelo)
summary(modelo2)

## Call:
## lm(formula = rating ~ length, data = Peliculas_modelo)

## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.9598 -0.6891  0.0337  0.7766  3.8511 

## Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 3.497857   0.123738   28.27   <2e-16 ***
## length      0.022826   0.001097   20.80   <2e-16 ***
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

## Residual standard error: 1.125 on 2197 degrees of freedom
## Multiple R-squared:  0.1645,	Adjusted R-squared:  0.1642 
## F-statistic: 432.7 on 1 and 2197 DF,  p-value: < 2.2e-16

Observamos que eliminando la variable budget nuestro indice r2 es un poco inferior, por tanto nos quedamos con el modelo 1.

Evaluación

Vamos con el análisis de los residuos para comprobar que nuestro modelo predice con una probabilidad lo suficientemente alta

#iniciamos el análisis de residuos obteniendo los residuos estándares del modelo ajustado y obteniendo un histograma, y el diagrama de cuantiles con el que veremos si cumple con una distribución normal

residuos<-rstandard(modelo1) # residuos estándares del modelo ajustado (completo) 

par(mfrow=c(1,1)) # divide la ventana en una fila y tres columnas 

qqnorm(residuos) # gráfico de cuantiles de los residuos estandarizados 
qqline(residuos)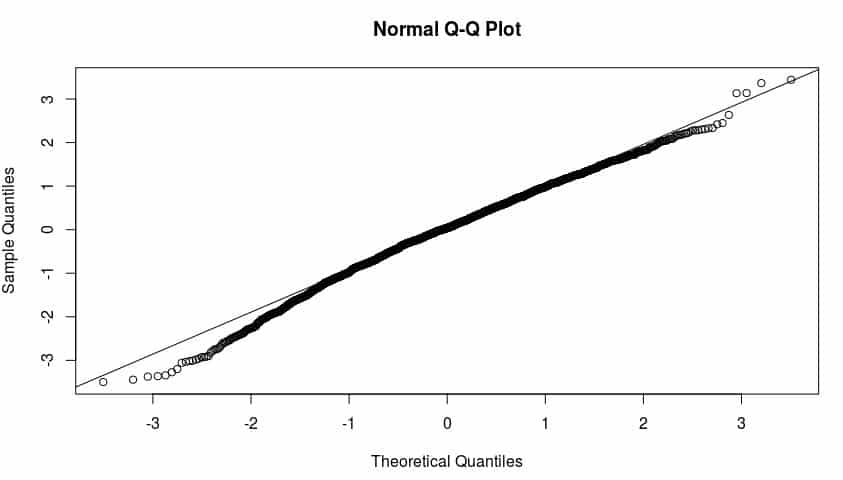  

residuos <- data.frame(residuos)

qplot(residuos, data=residuos,
      fill=I("black"), 
      col=I("black"),
      alpha=I(.2)) +
  labs(
    x = "residuos",
    y = "frecuencia"
  ) + 
  theme_minimal()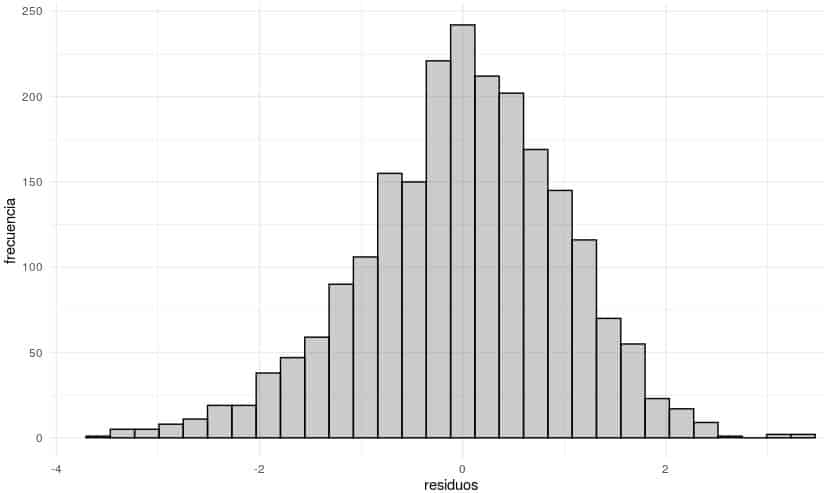 

Se observa una distribución normal de los residuos, por tanto es un modelo fiable.

vamos ahora a analizar la varianza de los residuos.

#Vamos a comprobar que los residuos siguen una varianza constante y que no existen patrones raros

ggplot(modelo1, aes(x = fitted.values(modelo1), y = rstandard(modelo1))) +
  geom_point( size=2 ) + 
  theme_minimal() +
  xlab("Valores ajustados") +
  ylab("Residuos estandarizados")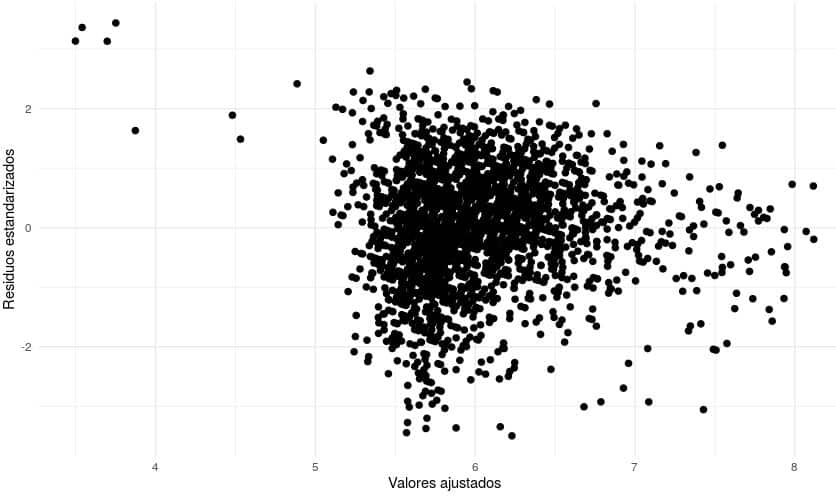

ggplot(Peliculas_modelo, aes(x = length, y = rstandard(modelo1))) +
  geom_point( size=2 ) + 
  theme_minimal() +
  xlab("Duración") +
  ylab("Residuos estandarizados")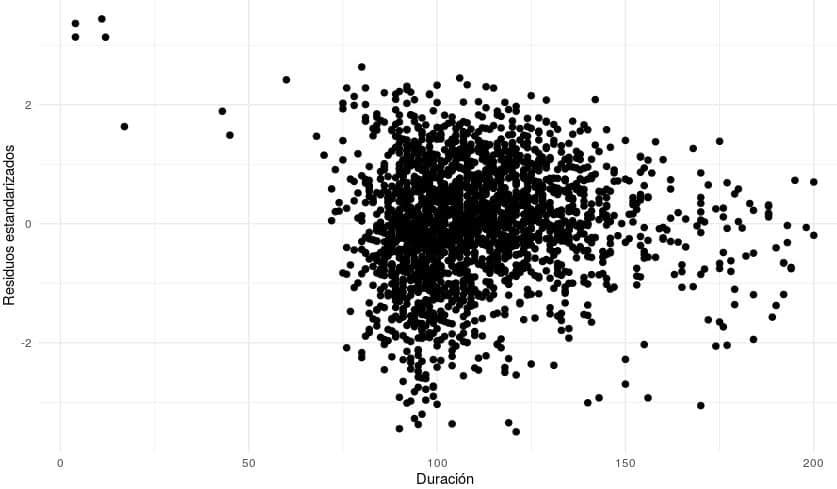

ggplot(Peliculas_modelo, aes(x = budget, y = rstandard(modelo1))) +
  geom_point( size=2 ) + 
  theme_minimal() +
  xlab("Presupuesto") +
  ylab("Residuos estandarizados")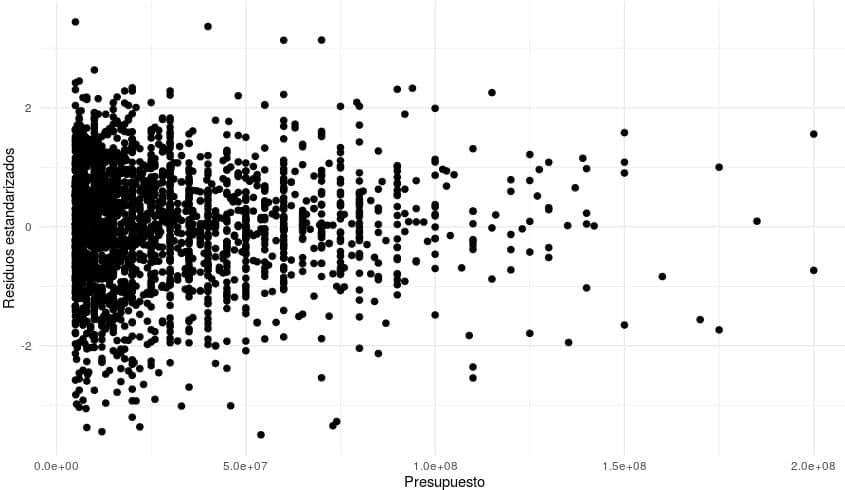

Se observa que la varianza de los residuos es constante, por tanto se confirma que es un modelo que hará buenas predicciones.

Predicciones

Vamos a realizar las predicciones con nuestro modelo, para nuestra predicción de ejemplo vamos a obtener la calificación de una película que dura 120 min y que tiene un presupuesto de 1000000 euros.

Rating_estimado <- data.frame(length=120, budget=1000000)

#Nos da una predicción con intervalo de confianza
prediccion <- predict(modelo1, Rating_estimado, interval= "confidence")
prediccion

##       fit      lwr      upr
## 1 6.280359 6.206674 6.354043

#Nos da el dato predecido
prediccionsimple <- predict(modelo1, Rating_estimado)
prediccionsimple

##        1 
## 6.280359 

Obtenemos una calificación para esta película de 6,28