Definición del perceptrón Multicapa

El percetrón multicapa evoluciona el perceptrón simple y para ello incorpora capas de neuronas ocultas, con esto consigue representar funciones no lineales.
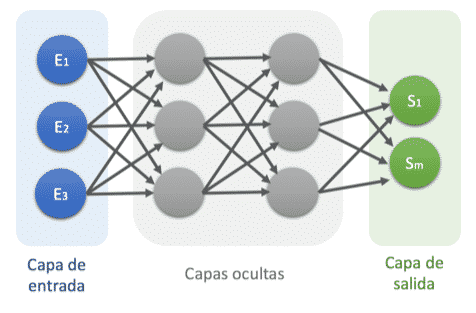
El perceptrón multicapa esta compuesto por por una capa de entrada, una capa de salida y n capas ocultas entremedias.
Se caracteriza por tener salidas disjuntas pero relacionadas entre sí, de tal manera que la salida de una neurona es la entrada de la siguiente.
En el perceptrón multicapa se pueden diferenciar una 2 fases:

1. Propagación en la que se calcula el resultado de salida de la red desde los valores de entrada hacia delante.
2. Aprendizaje en la que los errores obtenidos a la salida del perceptrón se van propagando hacia atrás (backpropagation) con el objetivo de modificar los pesos de las conexiones para que el valor estimado de la red se asemeje cada vez más al real, este aproximación se realiza mediante la función gradriente del error.

Arquitectura

Perceptron multicapa

Capa de entrada: conecta la red con el exterior, cada neurona se corresponde con cada una de las variables de entrada de la red.

Capas ocultas: son una aglomeración de capas en as que cada activación de una salida procede de la suma ponderada de las activaciones de la capa anterior conectadas, mas sus correspondientes umbrales (bias, sesgos).

Capa de salida: conecta las capas ocultas con la salida de la red que proporciona los resultados.