Introducción
En este post vamos a continuar estudiando el modelado de las series temporales como hicimos en el post Análisis de series temporales en R. ARIMA. En este post veremos un ejemplo en R de los modelos de Redes Neuronales Recurrentes de Elman y de Jordan.
MODELO ELMAN
En las redes de Elman, las entradas de estas neuronas, se toman desde las salidas de las neuronas de una de las capas ocultas, y sus salidas se conectan de nuevo en las entradas de esta misma capa, lo que proporciona una especie de memoria sobre el estado anterior de dicha capa. mas info
Para el ejemplo modelamos los datos de una serie temporal:
rawData=scan('https://www.diegocalvo.es/wp-content/uploads/2016/09/datos-serie-temporal.txt')
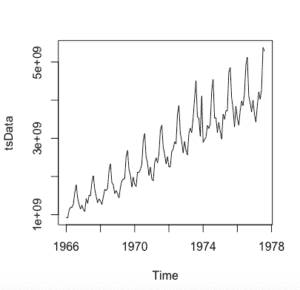
plot(rawData)
tsData = ts(RawData, start = c(1966,1), frequency = 12)
print(tsData)
plot(tsData)donde rawData son los datos univariantes que convertimos en serie temporal. start comienza el inicio de los tiempo de los datos, en este caso es enero de 1996 y como los datos son mensuales ‘frequency=12’.
Este es el estado del dataset:
Debemos cargas los paquetes que implementan estas redes neuronales. Vamos a usar la libreria RSNNS y una librería secundaria quantmod para otras operaciones:
require(RSNNS)require(quantmod)
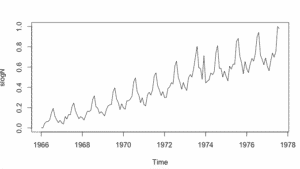
Para las redes neuronales necesitamos normalizar los datos de entrada para que tome valores entre 0 y 1
stsData<-as.ts(tsData,F)stsDataN<- (stsData-min(stsData))/(max(stsData)-min(stsData))plot(stsDataN)#definimos una conjunto de datos para train 90% y 10% para testset.seed(1)tamano_total <- length(stsDataN)tamano_train <- round(tamano_total*9/12, digits = 0)train <- 0:(tamano_train-1)test<-(tamano_train):tamano_total
Ahora lo que haremos será crear un data frame con n columnas, cada una de las cuales adelantada un valor de la serie en el futuro, a través de una variable de tipo zoo; equivalente a un periodo de retardo de la serie:
y<-as.zoo(stsDataN)x1<-Lag(y,k=1)x2<-Lag(y,k=2)x3<-Lag(y,k=3)x4<-Lag(y,k=4)x5<-Lag(y,k=5)x6<-Lag(y,k=6)x7<-Lag(y,k=7)x8<-Lag(y,k=8)x9<-Lag(y,k=9)x10<-Lag(y,k=10)x11<-Lag(y,k=11)x12<-Lag(y,k=12)slogN<-cbind(y,x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12)
Eliminamos los valores NA producidos al desplazar la serie:
stsDataN<-stsDataN[-(1:12),]
Y definimos, por comodidad, los valores de entrada y salida de la red neuronal:
inputs<-stsDataN[,2:13]
outputs<-stsDataN[,1]
Ahora ya podemos crear una red de Elman y entrenarla:
fit<-elman(inputs[train],outputs[train], size=c(9,2), learnFuncParams=c(0.1), maxit=5000)y<-as.vector(outputs[-test])plot(y,type="l")
El tercer parámetro de la función elman indica que hemos creado dos capas ocultas, una de nueve neuronas y otra de una, hemos indicado un ritmo de aprendizaje de 0,1 y también un número máximo de iteraciones de 5000.
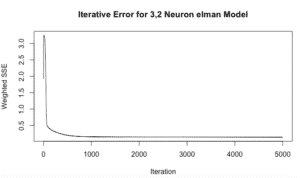
Con la función plotIterativeError podemos ver cómo ha ido evolucionando el error de la red con el número de iteraciones:
plotIterativeError(fit, main = "Iterative Error for 3,2 Neuron elman Model")Se puede observar que el error converge a cero muy rápidamente.
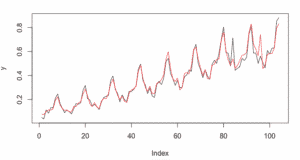
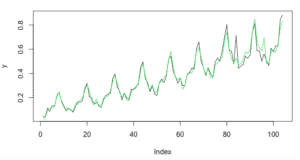
Una vez la red entrenada la probamos, haciendo una predicción con el resto de los términos de la serie, los datos seleccionados para test:
pred<-predict(fit,inputs[-test])lines(pred,col="red")
Como se puede observar la red predice bastante bien. Ahora gracias al efecto memoria vamos a adelantarnos a la serie al menos en un valor con una precisión muy buena. Para ello volvemos a introducir los datos de entrenamiento.
predictions<-predict(fit,inputs[-train])Y desnormalizamos los datos
valuesPred <- predictions*(max(stsData)-min(stsData)) + min(stsData)valuesPred
Ahora podemos ver la representación de los valores predecidos para el siguiente periodo:
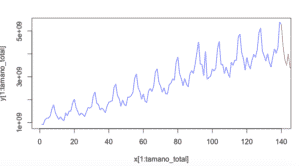
x <- 1:(tamano_total+length(valuesPred))y <- c(as.vector(tsData),valuesPred)plot(x, y)plot(x[1:tamano_total], y[1:tamano_total],col = "blue", type="l")lines( x[(tamano_total):length(x)], y[(tamano_total):length(x)], ,col="red")
En las redes de Jordan, la diferencia está en que la entrada de las neuronas de la capa de contexto se toma desde la salida de la red. Del mismo modo que hemos operado para la red neuronal Elman, sustituyendo el modelo, obtenemos el resultado para la red de Jordan.
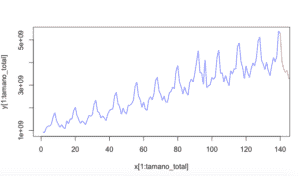
fit<-jordan(inputs[train],outputs[train],size=4,learnFuncParams=c(0.01),maxit=5000)La predicción para el modelo es:
El adelantamiento con este modelo queda de la siguiente forma:
Referencias:
Redes Neuronales Recurrentes y Series Temporales
Time series forecast with recurrent Elman network in neurolab




Excelente post Diego, muchas gracias por compartirlo. Una pregunta: ¿Cómo se trataría el tema de falta de datos o huecos? Lo digo porque yo tengo un ejemplo de datos en los que tengo varios datos faltantes y no se como afectaría esto al modelo…
Muchas gracias!
Un saludo
Hola Jose Manuel, gracias por tu comentario. Espero que te haya sido útil. Pues se me ocurre que para la falta de datos, se podría estudiar una regression lineal o logística.
Hola Diego, muy buen Post. Solo una duda, que pasaría con series de tiempo con eventos, que no necesariamente ocurren con una frecuencia definida?
Muchas gracias.
Tu post es bueno, dale una revisada, estuve con el libro y pude ver que en los comandos hubo pequeño error(que fácil se dan cuenta, pero los nuevos tendrán dificultades). Saludos
interesante el artículo. Sin embargo, no veo técnicas aplicadas de regularización que generalemnte para este tipo de modelos es necesario, como tampoco pruebas que permitan descartar overfiting o underfiting.
hola
probé el modelo elMan para predecir temperaturas en un mes pero los valores del pronóstico son mas de los 30 días, no se en que me estoy equivocando para determinar el pronóstico, me puedes colaborar por favor